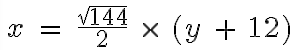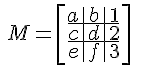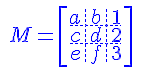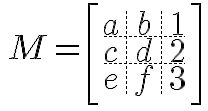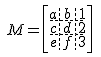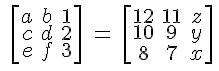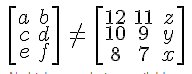Utilisation de la notation TeX
- Liens automatiques des activités
- MathJax
- Notation Algebra
- Convertir les URLs en liens et images
- Liaison automatique des bases de données
- Afficher les binettes sous forme d'images
- Protection des adresses de courriel
- Liaison automatique des glossaires
- Plugins multimédia
- Contenu multilingue
- Notation TeX
- HTML tidy
- Caviardage
TeX (/'tɛx/tekh', souvent prononcé TeK en anglais) est une façon très répandue et populaire de représenter la notation mathématique en utilisant uniquement des caractères que vous pouvez taper au clavier (voir Wikipedia). Cela en fait un format utile à utiliser dans Moodle, puisqu'il peut être entré n'importe où vous pouvez taper du texte, des messages du forum aux questions du test.
Les expressions TeX peuvent être saisies de plusieurs façons :
- en les tapant directement dans les textes.
- en utilisant l'éditeur Dragmath basé sur Java dans l'éditeur TinyMCE de Moodle.
- en utilisant l'éditeur d'équations HTML dans l'éditeur Atto de Moodle (depuis Moodle 2.7).
Ensuite, les expressions TeX sont rendues en notation mathématique :
- en utilisant le filtre TeX de Moodle, qui utilise un binaire TeX installé sur le serveur pour convertir les expressions en images .gif (ou si celui-ci n'est pas disponible, il revient à un simple binaire mimetex intégré).
- en utilisant le MathJax qui identifie les expressions TeX et utilise la bibliothèque Mathjax JS pour les rendre dans les navigateurs lors de leur affichage (depuis Moodle 2.7).
- en utilisant d'autres solutions tierces.
Comme vous pouvez l'imaginer, tout le domaine n'est pas aussi simple que nous le voudrions, surtout parce qu'il y a beaucoup de saveurs de TeX et de légères variations entre les outils.
Cette page se concentre uniquement sur l'utilisation de TeX dans Core Moodle. Voir les liens au bas de cette page pour plus d'informations sur la configuration des éditeurs et filtres TeX, y compris d'autres outils de la communauté Moodle qui peuvent convenir aux utilisateurs avancés.
AVERTISSEMENT : Cet environnement Wiki utilise un moteur de rendu TeX DIFFÉRENT pour Moodle, en particulier lorsqu'il s'agit de contrôler les séquences. C'est pour cette raison que des images sont parfois utilisées pour représenter ce à quoi il devrait ressembler dans Moodle. YMMMV.
Conventions linguistiques
Pour identifier une séquence TeX dans votre texte, entourez-la de marqueurs $$. Pour invoquer une séquence de commande ou de contrôle particulière, utilisez la barre oblique inverse, \. Une séquence de contrôle typique ressemble à :
$$ x\ =\ \frac{\sqrt{144}}{2}\ \times\ (y\ +\ 12) $$
| Fraction et racine carrée. |
Des espaces supplémentaires peuvent être placés dans l'équation en utilisant le \ sans caractère de fin.
Équation affichée sur sa propre ligne
Lorsqu'une équation est entourée d'une paire de marqueurs $$, elle est affichée centrée sur sa propre ligne. Les $$ sont des marqueurs TeX primitifs. Avec LaTeX, il est souvent recommandé d'utiliser la paire \[ et \] pour inclure des équations, plutôt que les marqueurs $$, car la nouvelle syntaxe vérifie les équations mal tapées et ajuste mieux l'espacement vertical. Si la notation TeX est activée, qui définit un moteur de rendu LaTeX, la même équation que ci-dessus est obtenue avec la séquence de commande suivante :
\[ x\ =\ \frac{\sqrt{144}}{2}\ \times\ (y\ +\ 12) \]
Cependant, si l'équation est mal tapée, elle sera affichée dans une case pour signaler l'erreur et si l'équation apparaît dans un nouveau paragraphe, l'espace vertical au-dessus de l'équation sera ajusté correctement.
Utiliser \[ ... \] au lieu de $$ ... $$ peut avoir d'autres avantages. Par exemple, avec l'éditeur d'équations Wiris installé, l'éditeur Atto transforme de façon indésirable le code TeX des équations incluses avec $$ en code XML, alors qu'il ne le fait pas lorsque les équations sont incluses avec \[ et \].
Équation affichée dans le texte
Lorsque la notation TeX est activée, une équation est affichée dans le texte lorsqu'elle est entourée par la paire \( et \). Par exemple, ce qui suit :
Le point \( \left( {{x}_{0}}+\frac{1}{p\left( {{x}_{0}} \right)}\ ,\ \frac{q\left( {{x}_{0}} \right)}{p\left( {{x}_{0}} \right)} \right) \) est situé...
s'affiche comme suit :
Notez que les marques $ peuvent ne pas fonctionner à cette fin.
Caractères et mots-clés réservés
La plupart des caractères et des chiffres du clavier peuvent être utilisés à leur valeur par défaut. Comme avec n'importe quel langage informatique, cependant, il y a un ensemble de caractères réservés et de mots-clés qui sont utilisés par le programme pour ses propres besoins. La notation TeX n'est pas différente, mais elle a un très petit nombre de caractères réservés. Il ne s'agit pas d'une liste complète des caractères réservés, mais certains d'entre eux le sont :
@ # $ % ^ & * ( ) .
Pour utiliser ces caractères dans une équation, placez simplement le \ devant eux comme \$ ou \%. Si vous voulez utiliser la barre oblique inverse, utilisez juste la barre oblique inverse. La seule exception semble être &, l'esperluette.
Transcriptions, indices et racines
Les exposants sont enregistrés à l'aide du signe d'insertion, ^, symbole. Un exemple pour un cours de mathématiques pourrait être :
$$ 4^2 \ \times \ 4^3 \ = 4^5 $$ This is a shorthand way of saying: (4 x 4) x (4 x 4 x 4) = (4 x 4 x 4 x 4 x 4) or 16 x 64 = 1024.
Les indices sont similaires, mais utilisent le caractère de soulignement.
$$ 3x_2 \ \times \ 2x_3 $$
C'est OK si vous voulez des exposants ou des indices, mais les racines carrées sont un peu différentes. Ceci utilise une séquence de commande.
$$ \sqrt{64} \ = \ 8 $$
Vous pouvez aussi aller un peu plus loin, mais en ajoutant un caractère de contrôle. Vous pouvez poser une question comme :
$$ If \ \sqrt[n]{1024} \ = \ 4, \ what \ is \ the \ value \ of \ n? $$
L'utilisation de ces différentes commandes vous permet de développer des équations comme :
$$ The \sqrt{64} \ \times \ 2 \ \times \ 4^3 \ = \ 1024 $$
Les exposants, les indices et les racines peuvent également être notés dans Matrices.
Fractions
Les fractions dans TeX sont en fait simples, tant que vous vous souvenez des règles.
$$ \frac{numerator}{denominator} $$ which produces .
Ceci peut être donné sous la forme :
.
Il est saisi sous la forme :
$$ \frac{5}{10} \ is \ equal \ to \ \frac{1}{2}.$$
Avec les fractions (comme avec d'autres commandes), les crochets bouclés peuvent être imbriqués de sorte que vous pouvez par exemple implémenter des exposants négatifs dans les fractions. Comme vous pouvez le voir,
$$\frac {5^{-2}}{3}$$ will produce
$$\left(\frac{3}{4}\right)^{-3}$$ will produce and
$$\frac{3}{4^{-3}}$$ will produce
Vous ne voulez probablement pas utiliser $$\frac{3}{4}^{-3}$$ car il produit
Vous pouvez également utiliser des fractions et des exposants négatifs dans Matrices.
Supports
Au fur et à mesure que les étudiants progressent en mathématiques, ils entrent en contact avec les parenthèses. La notation algébrique dépend fortement des crochets. Les valeurs de clavier habituelles ( et ) sont utiles, par exemple :
Ceci est écrit comme :
$$ d = 2 \ \times \ (4 \ - \ j) $$
Habituellement, ces parenthèses sont suffisantes pour la plupart des formules, mais elles ne le seront pas dans certaines circonstances. Considérez ceci :
C'est bon, mais essayez comme ça :
Ceci peut être réalisé par :
$$ 4x^3 \ + \ \left(x \ + \ \frac{42}{1 + x^4}\right) $$
Un simple changement en utilisant les symboles \left( et \right) à la place. Notez que la parenthèse réelle est à la fois nommée et présentée. Les parenthèses sont presque indispensables dans Matrices.
Ellipsis
L'Ellipsis est un code simple :
Écrit comme :
$$ x_1, \ x_2, \ \ldots, \ x_n $$
Une application plus pratique pourrait être :
Question :
"Additionnez tous les nombres de 1 38.
Quelle est la solution élégante et simple à ce problème ?
Pouvez-vous créer une fonction algébrique pour expliquer cette solution ?
Votre solution fonctionnera-t-elle pour tous les numéros ?"
Répondez : La question utilise un nombre pair pour démontrer un processus mathématique et générer une formule algébrique.
| Partie 1: | Partie 2. | Partie 3. |
|
|
Une fonction algébrique pourrait lire quelque chose comme :
Où t = total et n = dernier nombre. |
La solution est que, en utilisant les nombres les plus grands et les plus petits, les nombres sont additionnés puis multipliés par le nombre de combinaisons différentes pour obtenir le même résultat en ajoutant les premier et dernier nombres.
La réponse doit dépendre du nombre, étant un nombre entier. Par conséquent, la solution ne fonctionnera pas pour une plage de nombres impairs, mais seulement pour une plage paire. |
Symboles
Ce ne sont pas tous les symboles qui peuvent être disponibles dans la notation TeX de Moodle, juste ceux que j'ai trouvé pour travailler dans Moodle.
| \amalg | \cup | \oplus | \times | ||||
| \ast | \dagger | \oslash | \triangleleft | ||||
| \bigcirc | \ddagger | \otimes | \triangleright | ||||
| \bigtriangledown | \diamond | \pm | \odot | ||||
| \bigtriangleup | \div | \ominus | \wr | ||||
| \circ | \wedge | \vee | \sqcup | ||||
| \leq | \geq | \equiv | \prec | ||||
| \succ | \sim | \perp | \preceq | ||||
| \succeq | \simeq | \mid | \ll | ||||
| \gg | \asymp | \parallel | \subset | ||||
| \supset | \subseteq | \supseteq | \approx | ||||
| \neq | \ni | \notin | \in | ||||
| \vdash | \dashv | \bullet | \cdot |
Flèches
| \leftarrow | \longleftarrow | \Leftarrow | \Longleftarrow | ||||
| \rightarrow | \longrightarrow | \Rightarrow | \Longrightarrow | ||||
| \uparrow | \Uparrow | \downarrow | \Downarrow | ||||
| \leftrightarrow | \longleftrightarrow | \updownarrow | \Updownarrow | ||||
| \Leftrightarrow | \Longleftrightarrow | \leftrightharpoons | \Im | ||||
| \nearrow | \nwarrow | \swarrow | \searrow |
Délimiteurs et constructions mathématiques
REMARQUE : La plupart des délimiteurs et des constructions ont besoin de paramètres supplémentaires pour qu'ils apparaissent correctement.
| \{x | \} | \rangle | \langle | ||||
| \angle | \= | \sqrt{ab} | \sqrt[n]{ab} | ||||
| \frac{ab}{cd} | \backslash | \widehat{ab} | \$ | ||||
| \overline{ab} | \underline{ab} | \therefore | \ddots | ||||
| \% | \# | \vdots | \emptyset |
AVERTISSEMENTS : Le caractère & dans LaTeX nécessite généralement une barre oblique inverse, \. Dans la Notation TeX de Moodle, apparemment, ce n'est pas le cas. D'autres paquetages, AsciiMath, peuvent l'utiliser différemment à nouveau, alors soyez prudent en l'utilisant. Le personnage de copyright peut utiliser le jeu de caractères MimeTeX, et produit un avis de copyright pour John Forkosh Associates qui a fourni un grand nombre des paquetages essentiels pour la notation TeX pour Moodle, donc je comprends. J'ai été informé, de façon presque fiable, qu'une instruction particulière produira un avis différent... :)
Il y a aussi un certain nombre de caractères qui peuvent être utilisés dans TeX Notation for Moodle mais qui ne sont pas rendus dans cette page :
| Plus grands \gauche(x et \droite) parenthèses | |
| \widetilde{ab} | |
| \textdegree ou (50)^\circ |
Lettres grecques
| \alpha | \beta | \gamma | |||
| \delta | \epsilon | \zeta | |||
| \eta | \theta | \iota | |||
| \kappa | \lambda | \mu | |||
| \xi | \pi | \rho | |||
| \sigma | \tau | \upsilon | |||
| \phi | \chi | \psi | |||
| \omega | \Omega | \Theta | |||
| \Delta | \Pi | \Phi | |||
| \Gamma | \Lambda | \Sigma | |||
| \Psi | \Xi | \Upsilon | |||
| \vartheta | \varrho | \varphi | |||
| \varsigma |
Exceptions notables
Lettre grecque omicron (traditionnellement, les mathématiciens n'utilisent pas beaucoup l'omicron en raison de la confusion possible avec zéro). En termes simples, l'omicron minuscule est un "o" rouge o. Mais notez que \omicron peut maintenant fonctionner avec les récentes implémentations TeX, y compris MathJax.
Au moment d'écrire ces lettres majuscules grecques ne peuvent pas être rendues par TeX Notation dans Moodle :
Alpha, Beta, Zeta, Eta, Tau, Chi, Mu, Iota, Kappa et Epsilon.
La notation mathématique TeX adopte la convention selon laquelle les symboles grecs minuscules sont affichés en italique tandis que les symboles grecs majuscules sont affichés en caractères droits. Par conséquent, les majuscules grecques manquantes peuvent simplement être représentées par l'équivalent \mathrm{ }.
Algèbre Booléenne
Il existe un certain nombre de conventions différentes pour représenter l'algèbre booléenne (logique). Les conventions courantes utilisées en informatique et en électronique sont détaillées ci-dessous :
Négation, NOT, ¬, !, ~, −
\lnot, !, \sim, \overline{ }
Conjonction, AND, ∧,
\land, \wedge, \cdot
Disjonction, OR, ∨, +,
\lor, \vee, +
Disjonction exclusive, XOR ⊻, ⊕
\veebar, \oplus
Équivalence, Si et seulement si, Iff, ≡, ↔, ⇔
\equiv, \leftrightarrow \iff
Exemple: deux représentations des lois de De Morgan :
$$ A \cdot B = \overline{\overline{A} + \overline{B}} SS
$$ (A \land B) \equiv \lnot(\lnot{A} \lor \lnot{B}) $$
Polices
Pour utiliser une police particulière, vous devez accéder à la police en utilisant la même syntaxe que celle décrite ci-dessus.
Une police calligraphique mathématique :
ou
$$ \mathcal{ABCDEFGHIJKLMNOPQRSTUVXYZ}$$
Tableau noir gras, police de caractères Castellar :
ou
$$ \mathbb{ABCDEFGHIJKLMNOPQRSTUVXYZ}$$
Souvent utilisé en théorie des nombres. Par exemple : = ensemble de nombres naturels incluant 0 {0, 1, 2, 3, ...}, = ensemble d'entiers {-..., -3, -2, -1, 0, 1, 2, 3,... = ensemble de nombres rationnels, y compris les nombres entiers, = ensemble de nombres réels, qui comprend les nombres naturels, rationnels et irrationnels.
Fraktur, une police de caractères Old English :
ou
$$ \mathfrak{ABCDEFGHIJKLMNOPQRSTUVXYZ}$$
C'est différent dans la notation Tex dans Moodle que pour d'autres paquetages TeX complets.
Une police italique :
ou
$$ \mathit{ABCDEFGHIJKLMNOPQRSTUVXYZ} $$
Une police normale, verticale, non italique, romaine :
ou
$$ \mathrm{ABCDEFGHIJKLMNOPQRSTUVXYZ} $$
Une police de caractères gras :
ou
$$ \mathbf{ABCDEFGHIJKLMNOPQRSTUVXYZ} $$
Taille des écrans
La taille par défaut est légèrement supérieure à la taille de police normale. La notation TeX dans Moodle utilise huit tailles différentes allant de "minuscule" à "énorme". Cependant, ces valeurs semblent signifier des choses différentes et dépendent, je suppose, de la résolution de l'écran de l'utilisateur. Les tailles peuvent être notées de quatre façons différentes :
| \fontsize{0} to \fontsize{7} | $$\fontsize{2} x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12)$$ | |
| \fs{0} to \fs{7} | $$\fs{4} x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12)$$ | |
| \fs0 to \fs7 | $$\fs6 x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12)$$ | |
| Vous pouvez aussi bien utiliser \tiny \small
\normalsize \large \Large \LARGE \huge \Huge |
$$\normalsize x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12)$$ |
Il semble que la notation TeX dans Moodle permet maintenant à \fs6, \fs7, \huge et \Huge d'être correctement rendu.
Couleur
| $$ \red x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12) $$ | |
| $$ \blue x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12) $$ | |
| $$ \green x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12) $$ | |
| $$ \red x \ = \ \frac{\sqrt{144}}{2}$$ $$ \times $$
$$\green (y \ + \ 12) $$ $$ \ = $$ $$ \ \blue 6^3 $$ |
Note de Moodle 2.2 : Il se peut que vous trouviez que cela ne fonctionne pas pour vous. Vous pouvez essayer d'ajouter "\usepackage{color}" à votre notation textuelle "LaTeX preamble" (sous Site adminstration/Plugins/Filters/TeX notation) et ensuite utiliser cette nouvelle syntaxe :
Vous pouvez noter que cette dernière est beaucoup plus complexe que la précédente pour les couleurs. La notation TeX sous Windows n'autorise pas les équations multicolores, si vous nommez un certain nombre de couleurs dans l'équation, seule la dernière nommée sera utilisée.
Formes géométriques
Il y a deux façons de produire des formes géométriques, l'une avec des cercles et l'autre avec des lignes. Chacun d'entre eux demande un peu de pratique pour bien faire les choses, mais ils peuvent fournir une géométrie simple. Il peut être plus facile de produire les formes dans Illustrator ou Paint Shop Pro ou tout autre logiciel de dessin et de les utiliser pour illustrer vos leçons, mais parfois, certains diagrammes simples dans Moodle feront un meilleur travail.
Cercles
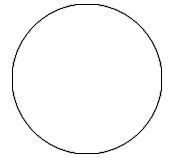
Les cercles sont faciles à faire.
| Les cercles sont faciles à créer et n'ont besoin que d'un nombre pour déterminer la taille du cercle.
Pour créer le cercle, utilisez $$ \circle(150) $$. Cela fait un cercle de 150 pixels de diamètre. |
Création d'arcs
Les arcs sont également faciles à produire, mais nécessitent quelques paramètres supplémentaires. La même structure de code utilisée dans les cercles crée la forme de base, mais l'inclusion d'un point de départ et d'un point d'arrivée ne crée que l'arc. Cependant, notez où se trouve le point 0, non pas au Nord véritable, mais plutôt à l'Est et courez dans le sens inverse des aiguilles d'une montre.
| $$ \circle(120;90,180)$$ | $$ \circle(120;0,90)$$ | ||
| $$ \circle(120;180,270)$$ | $$ \circle(120;270,360)$$ |
Cette structure se décompose en la commande \circle suivie du diamètre, et non du rayon, du cercle, suivi d'un point-virgule, puis de la démarcation de l'arc, de la nomination des points de départ et d'arrivée en degrés à partir du point de départ 0, Est. Notez que la toile est la taille du diamètre désigné par les paramètres du cercle.
La commande \picture
L'utilisation de cercles et d'arcs comme illustré ci-dessus est quelque peu restrictive. La commande \picture vous permet d'utiliser un cadre pour construire une image de plusieurs calques. Chaque partie de l'image doit cependant être dans son propre espace, et bien que ce cadre vous permette d'être créatif, dans une certaine mesure, il existe des règles très dures et rapides pour l'utiliser.
Tous les éléments d'une image doivent être situés dans le cadre de l'image. Des résultats inattendus se produisent lorsque des parties d'un arc, par exemple, passent au-dessus de la bordure du cadre. (C'est particulièrement vrai pour les lignes, que nous aborderons plus loin, et les conséquences de ce franchissement de la frontière peuvent poser de sérieux problèmes).
La commande \picture est structurée comme suit :
\picture(100){(50,50){\circle(200)}}
\command(size of frame){(x co-ordinate, y co-ordinate){\shape to draw(size or x co-ordinate, y co-ordinate)})
REMARQUE : L'accolade est utilisée pour entourer chaque ensemble de coordonnées de point de départ requises. À l'intérieur de chaque ensemble d'accolades, un autre ensemble d'accolades est utilisé pour isoler chaque ensemble de coordonnées de l'autre, et ces coordonnées utilisent leurs propres crochets et antislash. Comptez les supports d'ouverture et de fermeture, faites attention à la position,
| $$ \picture(100){(50,50){\circle(200)}}&&
Le cadre photo réunit des éléments que vous ne verriez peut-être pas autrement. En raison de la taille du cadre de 100px et du point central du cercle au milieu du cadre, le cercle de 200px sera écrasé. Des résultats inattendus se produisent lorsque les tailles ne sont pas correctes. |
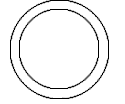
En utilisant le cadre de l'image, vous pouvez superposer des cercles et des lignes l'une au-dessus de l'autre, ou ils peuvent se croiser. $$ \picture(100){(50,50){\circle(99)} (50,50){\circle(80)}} $$ | ||
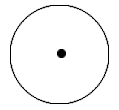
| Vous voudrez peut-être voir l'image d'un cercle avec un point au milieu.
Vous devrez peut-être essayer de placer correctement le point central, mais l'option l'ordre des éléments dans l'image peut avoir un impact. $$ \picture(100){(48,46){\bullet}(50,50){\circle(99)}} $$ |
En utilisant les mêmes idées que ci-dessus, vous pouvez faire des demi-cercles.
$$\picture(150){(50,50){\circle(100;0,180)}(100,50){\circle(100;180,360)}}$$ |
Lignes
AVERTISSEMENT : Dessiner des lignes dans la Notation TeX dans Moodle est un problème, allez à la page Utilisation de la notation textuelle pour plus d'informations. Si la ligne n'est pas notée correctement, l'analyseur tentera de la tracer correctement mais ne la complétera pas avec succès. Cela signifie que chaque image qui doit être dessinée sera dessinée jusqu'à ce qu'elle touche l'erreur. Lorsque l'erreur est en cours de conversion, elle échoue, de sorte qu'aucune image suivante n'est dessinée. Soyez prudent et assurez-vous que votre ligne fonctionne AVANT de passer au problème suivant ou à l'image suivante.
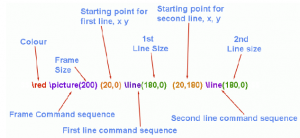
| $$\red \picture(200){(20,0){ \line(180,0)}{(20,180){\line(180,0}$$
La structure de la boîte à images est que le \picture(200) fournit un modèle d'image carré. Le (20,0) fournit les coordonnées de départ pour toute ligne suivante. Dans ce cas, le point de départ est à 20 pixels sur l'axe des x et à 0 pixel sur l'axe des y. Le point de départ de toutes les coordonnées, 0,0, est le coin inférieur gauche et elles se déplacent dans le sens horaire. "'Ne pas confondre ça avec des arcs. La ligne \line(180,0) détermine la longueur et l'inclinaison de la ligne. Dans ce cas, l'inclinaison est 0 et la longueur est de 180px. Celles-ci sont enfermées dans des accolades, toutes à l'intérieur d'un ensemble d'accolades appartenant à la séquence de contrôle \picture(). L'ensemble suivant de commandes est le même, c'est-à-dire que les (20 200) sont les coordonnées de la ligne suivante. La coordonnée x est la 20, c'est-à-dire la distance à droite du point 0. Les coordonnées y sont la distance à partir du bas de l'image. Alors que la première ligne a commencé et s'est déroulée au bas du cadre de l'image, la coordonnée y commence à la marque de 200 pixels du bas de l'image. La ligne, d'une longueur de 180 pixels, n'a pas de pente y. Cela crée une paire de lignes parallèles étalées. |
Bien que cela explique la structure d'une ligne, il y a quelques éléments que vous devez passer à travers pour en faire plus avec eux.
Carrés et rectangles
Les carrés et les rectangles sont similaires, mais légèrement différents.
Il devrait y avoir un outil de boîte carrée, et il y en a un, mais à moins qu'il n'y ait quelque chose dedans, il ne s'affiche pas. Il est en fait plus facile de faire un carré en utilisant la commande \line.
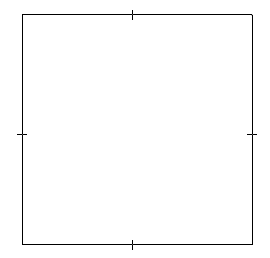
| Cette boîte est construite en utilisant :
$$ \picture(250){(10,10){\line(0,230)}(10,10){\line(230,0)}(240,10){\line(0,230)}(10,240){\line(230,0)}}$$ Il s'agit d'une boîte carrée de 250 pixels avec un carré de 230 pixels à l'intérieur. |
Cette boîte est différente en ce sens qu'elle a les mêmes indicateurs de longueur qui sont utilisés dans un carré.
$$ \picture(250){(10,10){\line(0,230)} (5,120){\line(10,0)} (10,10){\line(230,0)} (120,5){\line(0,10)} (240,10){\line(0,230)} (235,120){\line(10,0)} (10,240){\line(230,0)} (120,235){\line(0,10)}}$$ | ||
| Le rectangle devient alors la même chose, mais avec un côté plus court. Pour un portrait sur toile, ce serait :
$$ \picture(250){(10,10){\line(0,230)}(10,10){\line(150,0)}(160,10){\line(0,230)}(10,240){\line(150,0)}}$$ |
Le rectangle peut également produire une forme de paysage :
$$ \picture(250){(10,10){\line(0,160)}(10,10){\line(230,0)}(240,10){\line(0,160)}(10,170){\line(230,0)}}$$ |
Contrôle des angles
Contrôler les angles est un peu différent. Ils impliquent une perception différente, mais pas une perception inconnue. Considérez ceci :
Nous avons un point à partir duquel nous voulons tracer une ligne qui est sur un angle. La notation utilisée à ce stade peut être positive, positive ou positive, négative ou négative, positive ou négative, positive ou négative, négative. Pensez à un plan numérique ou à un graphique, en utilisant des nombres dirigés. Le point 0,0 se trouve au centre, et nous avons quatre quadrants autour de lui qui nous donnent l'un des résultats mentionnés précédemment.
| $$\picture(100){(50,50){\line(40,45)}}$$,
un x positif et un y positif | |
| $$\picture(100){(50,50){\line(-40,45)}}$$
un x negatif et un y positif | |
| $$\picture(100){(50,50){\line(-40,-45)}}$$
un x negatif et un y negatif | |
| $$\picture(100){(50,50){\line(40,-45)}}$$
un x positif et un y negatif |
Essentiellement, ces points se résument à ce que tout ce qui se trouve au-dessus du point d'insertion est positif sur l'axe des y, tout ce qui se trouve en dessous est négatif. Tout ce qui se trouve à gauche du point d'insertion est négatif alors que tout ce qui se trouve à droite est positif.
| $$\picture(100){(50,50){\line(40,45)}(50,50){\line(-40,45)}(50,50){\line(-40,-45)}(50,50){\line(40,-45)}}$$
Le processus d'alignement des coordonnées dans TeX n'est pas si bon que vous pouvez utiliser un ensemble de coordonnées comme point de départ unique pour toutes les lignes. La superposition de chaque objet varie en fonction de la position de l'objet précédent, de sorte que chaque objet doit être placé exactement. Cette structure de coordonnées a beaucoup d'impact sur les lignes qui se croisent, les lignes parallèles et les triangles. |
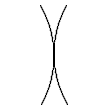
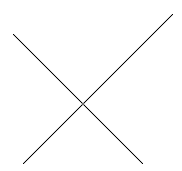
Lignes d'intersection
Vous pouvez mettre en place une paire qui se croise assez facilement, en utilisant la séquence de contrôle \picture.
| $$ \picture(200){(10,0){\line(150,150)} (0,130){\line(180,-180)}} $$
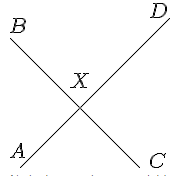
Les lignes qui sont tracées peuvent être étiquetées. $$ \picture(200){(10,0){\line(150,150)}(0,130){\line(180,-180)} (0,10){A}(0,135){B}(140,0){C}(140,150){D}(62,80){X}} $$ Pour produire une autre image. |
||
| À laquelle vous voudrez peut-être poser la question :
$$The \ \angle \ of \ AXB \ is \ 72\textdegree. \ What \ is \ the \ value \ of \ \angle BXD? $$ REMARQUE : L'étiquetage de cette image, en haut à droite, s'est avéré assez simple. Le décalage de quelques pixels au début ou à la fin des lignes s'est avéré être une stratégie efficace. Le point X s'est avéré un peu plus problématique et a nécessité un certain nombre d'ajustements avant d'aboutir. L'expérience acquise ici sera utile. | ||
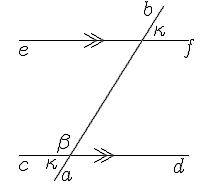
| Avec les étiquettes, le dessin peut ressembler un peu plus à votre dessin géométrique traditionnel, mais le diable est dans les détails. Les marqueurs parallèles doivent être placés correctement, et c'est là que l'expérience entre vraiment en jeu. Sur les lignes verticales ou horizontales, vous pouvez utiliser les symboles > ou < directement depuis le clavier, ou les symboles ou . Dans les deux cas, vous devez les positionner correctement.
Le code: $$\picture(200){(15,45){\line(170,0)} (15,30){c}(170,28){d}(15,160){\line(170,0)}(15,145){e}(180,143){f}(50,20){\line(110,175)}(58,20){a}(140,185){b}(42,32){\kappa}(53,48){\beta} (150,165){\kappa} (90,38){\gg}(80,153){\gg} }$$ |
||
Lignes et arcs
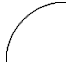
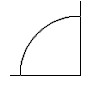
La combinaison de lignes et d'arcs est en fait un défi de taille, à plusieurs niveaux. Par exemple, prenons un arc de cercle à partir de la première page sur les cercles.
| Assez inoffensif en soi, mais lorsque nous commençons à y ajouter des éléments, cela change radicalement.
$$ \circle(120;90,180) $$ | |
| $$\picture(150){(75,75){\circle(120;90,180)}(75,75){\line(-70,0)}(75,75){\line(0,75)}} $$
Tous les éléments de ce dessin commencent au même endroit. Chacune d'entre elles est stratifiée et correctement placée sur la toile, et l'utilisation de la même coordonnée pour commencer permet de les contrôler facilement. Quelle que soit la taille de l'arc, les lignes qui se croisent peuvent toutes être tracées en utilisant les coordonnées centrales de l'arc. |
Triangles
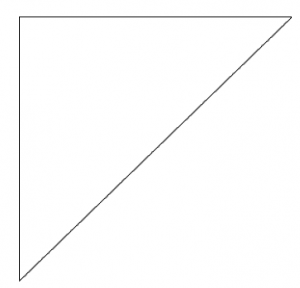
De tous les objets de dessin, ce sont en fait les triangles qui présentent le plus de difficultés. Par exemple :
|
$$\picture(350){(10,10){\line(0,320)}(10,330){\line(330,0)}(10,10){\line(330,320)}}$$ |
Il s'agit d'un triangle simple, qui nous permet d'établir un ensemble de règles simples pour les parties. La verticale a toujours une coordonnée x=0 et l'horizontale a toujours une coordonnée y=0.
Dans ce cas, avec une valeur x de 330 sur l'horizontale et une valeur y de 320 sur la verticale, l'hypoténuse devrait alors avoir une valeur x=340, et l'y=330, mais pas ainsi, ils ont réellement un x=330 et un y=320. Il n'est pas nécessaire d'ajouter les coordonnées du point de départ aux valeurs x et y de la ligne. |
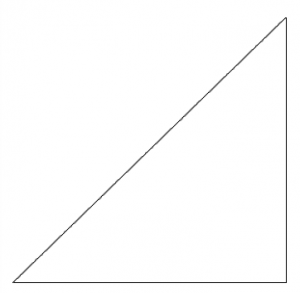
$$picture(350){(10,10){\line(330,0)}(340,10){\line(0,320)}(340,330){\line(-330,-320)}}$$ |
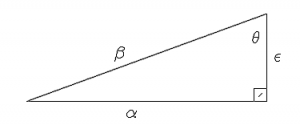
Ce triangle a été développé pour une page de trigonométrie - mais la notation supplémentaire devrait vous donner un aperçu de la façon dont vous pouvez l'utiliser.
| C'est une image étiquetée, mais il y a une \fbox dedans avec sa petite ligne. Avec un certain effort, il pourrait être remplacé par deux lignes courtes qui se croisent.
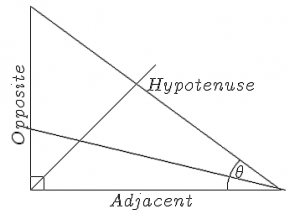
$$\picture(350,150){(25,25){\line(300,0)}(325,25){\line(0,110)}(25,25){\line(300,110)}(309,25){\fbox{\line(5,5)}} (307,98){\theta}(135,75){\beta}(150,5){\alpha}(335,75){\epsilon}}$$ |
| Le triangle montre comme : | Nous utilisons les différents éléments du triangle pour identifier les choses que nous devons savoir sur un triangle rectangle.
L'hypoténuse est toujours le côté opposé à l'angle droit. Le côté le plus long est toujours l'Hypoténuse. Pour identifier les autres éléments du triangle, nous recherchons le signe . est le point de départ pour nommer les autres côtés. Le côté opposé à est connu sous le nom d'Opposé. Le côté qui se trouve à côté de est connu comme le côté adjacent. Pour déterminer laquelle est laquelle, tracez une ligne qui divise et la ligne qu'elle traverse est le côté opposé. |
| Le code:
$$ \picture(350,250){(25,25){\line(300,0)}(25,25){\line(0,220)}(25,245){\line(300,-220)}(310,25){\circle(100;135,180)}(20,100){\line(310,-75)} (25,25){\fbox{\line(5,5)}}(25,25){\line(150,150)}(165,140){Hypotenuse}(120,2){Adjacent}(2,80){\rotatebox{90}{Opposite}}(270,40){\theta}}$$ | |
Matrices
Une matrice est un tableau rectangulaire de nombres disposés en rangées et en colonnes qui peut être utilisé pour organiser l'information numérique. Les matrices peuvent être utilisées pour prédire les tendances et les résultats dans des situations réelles c'est-à-dire les sondages.
Une matrice
Une matrice peut être écrite et affichée comme
.
Dans ce cas, la matrice est construite à l'aide des crochets avant de créer le tableau :
$$ M = \left[\begin{array}{ccc} a&b&1 \ c&d&2 \ e&f&3\end{array}\right] $$
La structure interne du réseau est générée par le &, l’esperluette et le double backslash.
Vous pouvez également créer une grille pour la matrice.
| Une ligne en pointillés | Une ligne pleine | Une ligne mixte |
| $$ M = \left[\begin{array}{c.c.c} a&b&1 \ \hdash c&d&2 \ \hdash e&f&3\end{array}\right] $$ | c|c} a&b&1 \ \hline c&d&2 \ \hline e&f&3\end{array}\right] $$ | c} a&b&1 \ \hline c&d&2 \ \hdash e&f&3\end{array}\right] $$ |
Les séquences de commandes ici sont {c|c.c} et \hdash et \hline. Le tuyau, | et le point final déterminent le type de ligne pour la ligne verticale.
Les matrices répondent également à d'autres commandes de Notation TeX telles que la taille et la couleur.
|
Couleur |
Size | |
| $$ \blue M = \left[\begin{array}{c.c.c} a&b&1 \ \hdash c&d&2 \ \hdash e&f&3\end{array}\right] $$ | $$ \fs7 M = \left[\begin{array}{c.c.c} a&b&1 \ \hdash c&d&2 \ \hdash e&f&3\end{array}\right] $$ | $$ \fs2 M = \left[\begin{array}{c.c.c} a&b&1 \ \hdash c&d&2 \ \hdash e&f&3\end{array}\right] $$ |
Créer des matrices égales et inégales
Les matrices égales et inégales sont simplement des matrices qui partagent ou non le même nombre de lignes et de colonnes. Pour être plus précis, les matrices égales partagent le même ordre et chaque élément dans les positions correspondantes est égal. Tout le reste n'est que des matrices inégales.
En fait, les matrices égales et inégales sont construites le long de lignes similaires, mais ont des formes différentes :
| Matrice égale | Une matrice inégale |
| $$ \left[\begin{array} a&b&1 \ c&d&2 \ e&f&3\end{array}\right] \ = \ \left[\begin{array} 12&11&z \ 10&9&y \ 8&7&x\end{array}\right] $$ | $$ \left[\begin{array} a&b \ c&d \ e&f \end{array}\right] \ \neq \ \left[\begin{array} 12&11&z \ 10&9&y \ 8&7&x\end{array}\right] $$ |
Étiquetage d'une matrice
Les matrices d'addition et de soustraction sont de nouveau similaires, mais la présentation est généralement très différente. Le problème vient lorsqu'on essaie de mélanger des étiquettes dans des tableaux. Le manque de sophistication de la notation TeX joue ici contre elle.
Moodle permet une adoption facile des tables pour le faire fonctionner. Par exemple :
Bill le boulanger fournit trois magasins, A, B et C en tartes, pâtés et rouleaux de saucisses. Il devrait déterminer le niveau des stocks de ces trois magasins dans son estimation des approvisionnements.
Il est préférable d'utiliser l'éditeur Moodle Fullscreen pour cela, pour avoir une meilleure idée de l'aspect du produit final et pour tirer parti des outils supplémentaires disponibles. Les décisions de conception doivent occuper notre attention pendant un certain temps. Nous avons besoin d'un tableau de cinq lignes et quatre colonnes. La première ligne est une ligne d'en-tête, donc l'étiquette est centrée. La rangée suivante a besoin de quatre colonnes, une cellule vierge pour commencer et les étiquettes A, B et C. Les trois rangées suivantes sont divisées en deux colonnes, avec les étiquettes, tartes, pâtés et rouleaux de saucisses dans chaque ligne de la première colonne et la matrice réside dans un ensemble fusionné de colonnes. D'abord la table :
| Insérer tableau, propriétés initiales | Bouton Fusionner les cellules | Propriétés avancées |
| .Vous pouvez avoir besoin de regarder dans les propriétés avancées des tables et des cellules pour que cela fonctionne. | ||
Voici le résultat immédiat
Bien qu'il ne soit pas très beau, il peut être amélioré en ajustant la table à l'aide des boutons de paramètres et de propriétés avancés et vous pouvez ensuite ajuster la matrice elle-même.
Modification de la matrice
Les choses ne sont pas toujours ce qu'elles semblent être, soyez conscient, le "c" ne signifie pas "colonne", il signifie en fait "centre". Les colonnes sont alignées par les lettres l, pour gauche, c pour centre et r pour droite.
Chaque colonne est répartie sur 50 pixels, la valeur de 50 est donc entrée dans la déclaration d'alignement. Le signe plus avant la valeur est utilisé pour "propager" ou pour forcer la valeur sur toute la matrice, mais n'est pas utilisé lorsque l'on veut séparer une seule colonne.
Définir les lignes est un peu plus problématique. La lettre C en majuscule indique l'alignement vertical par rapport au centre (B correspond à la ligne de base, mais cela ne garantit pas que les chiffres apparaîtront sur la ligne de base, et il ne semble pas y avoir de troisième valeur). Le signe plus et la valeur suivante règlent la hauteur de toutes les lignes au nombre indiqué. Je lui ai donné une valeur de 25 pixels pour l'ensemble de la matrice. S'il y avait quatre ou cinq rangées, la même hauteur est exigée.
L'ordre dans lequel les choses apparaissent est également important. Si vous modifiez l'ordre de ces paramètres, soit ils ne fonctionneront pas du tout, soit ils ne seront pas rendus comme vous l'attendez. Si quelque chose ne fonctionne pas correctement, vérifiez d'abord que vous avez le bon ordre.
Une matrice d'addition
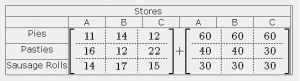
La règle pour effectuer des opérations sur des matrices est qu'elles doivent être des matrices égales. Par exemple, les matrices d'addition ressemblent à :
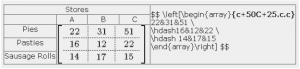
avec des résultats évidents. Le code est :
$$\left[\begin{array}{c+50C+25.c.c}
11&14&12 \ \hdash16&12&22 \ \hdash 14&17&15
\end{array}\right] + \left[\begin{array}{c+50C+25.c.c}
60&60&60 \ \hdash 40&40&30 \ \hdash 30&30&30
\end{array}\right] $$
Une matrice de soustraction
Semblable à une matrice d'addition dans sa construction, la matrice de soustraction est soumise aux mêmes règles d'égalité.
En utilisant les mêmes données essentielles, nous pouvons calculer les ventes quotidiennes de chacun des magasins.
Le code est :
$$ \left[\begin{array}{c+50C+25.c.c}
72&95&68 \ \hdash 54&61&65 \ \hdash 48&51&60
\end{array}\right] - \left[\begin{array}{c+50C+25.c.c}
11&14&12 \ \hdash 16&12&22 \ \hdash 14&17&15
\end{array}\right] = \left[\begin{array}{c+50C+25.c.c}
61&81&56 \ \hdash 38&49&43 \ \hdash 34&34&48
\end{array}\right] $$
Ce code semble plus complexe qu'il ne l'est réellement, il est encombré par les lignes et les séquences d'alignement.
Matrices de multiplication
Différente des matrices d'addition ou de soustraction, la matrice de multiplication se compose de trois parties : la matrice de lignes, la matrice de colonnes et la matrice de réponses. Cela implique qu'il a une méthodologie de construction différente.
Et le code pour cela est :
$$ \begin{array} 10&14&16\end{array} \
\left[\begin{array} 45 \\ 61 \\ 19 \end{array}\right]
\ = \ \begin{array} 450&854&304\end{array} $$
Bien que différente, elle n'est pas nécessairement plus complexe. Par exemple un problème comme :
Bill le boulanger vend son produit à Con le propriétaire du café, qui veut s'assurer que ses prix globaux sont rentables pour lui-même. Con doit s'assurer que son prix moyen lui permet d'obtenir suffisamment d'argent. pour pouvoir garder les cafés ouverts. Con fait ses calculs sur une base hebdomadaire, en comparant le coût aux prix de vente.
Avec les tartes, les pâtés et les rouleaux de saucisses dans cet ordre, il les applique aux colonnes du coût et du prix de vente :
Le code pour cela est :
$$\left[\begin{array} 350&310&270 \end{array}\right] \
\left[\begin{array} \$2.10&\$3.60 \ \$2.05&\$3.60 \ \$1.90&\$3.10 \end{array}
\right] \ = \ \left[\begin{array} \$735.00&\$1260.00 \ \$635.50&\$1116.00 \
\$513.00&$\837.00 \end{array}\right] $$
Voir aussi
- FAQ sur les outils mathématiques
- MathJax disponible dans Moodle 2.7 et versions ultérieures
- Notation TeX Pour activer la Notation TeX
- Dragmath
- Notation chimique mhchem



![{\displaystyle If\ {\sqrt[{n}]{1024}}\ =\ 4,\ what\ is\ the\ value\ of\ n?}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/de3f744b77dec1df89882f592e0ac60db89f63ec)






































































































![{\displaystyle {\sqrt[{n}]{ab}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/bbdd8f05f4d794abf4cccf685bf65c5f5776b98b)