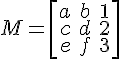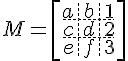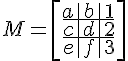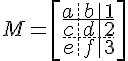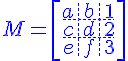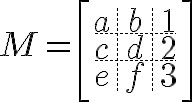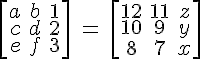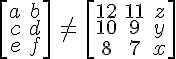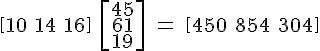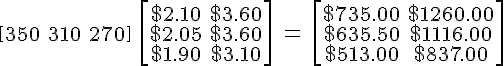注:このページは進行中です。 フィードバックと提案された改善は大歓迎です。 [ http://moodle.org/course/view.php?id=5 moodle.orgのディスカッションに参加してください]またはページコメント。
TeX( /'tɛx/tekh、英語でTeKと発音されることが多い)は、キーボードで入力できる文字のみを使用して数学表記を表す非常に広く普及している方法です(Wikipedia)。これにより、フォーラムの投稿から小テストの問題まで、テキストを入力できる場所ならどこにでも入力できるため、Moodleで使用するのに便利な形式になります。
TeX式は、複数の方法で入力できます。
- テキストに直接入力します。
- MoodleのTinyMCEエディタでJavaベースのDragmathエディタを使用する。
- MoodleのAttoエディタでHTMLベースの数式エディタを使用する(Moodle2.7以降)。
その後、TeX式は数学表記にレンダリングされます。
- サーバにインストールされたTeXバイナリを使用して式を.gif画像に変換するMoodleのTeXフィルタを使用します(または、それが利用できない場合は、単純な組み込みのmimetexバイナリにフォールバックします)。
- TeX式を識別し、Mathjax JSライブラリを使用して表示時にブラウザでレンダリングするMathJaxフィルタを使用する(Moodle2.7以降)。
- 他のサードパーティソリューションを使用する。
ご想像のとおり、特にTeXには多くのフレーバーがあり、ツールによってわずかな違いがあるため、フィールド全体は私たちが望むほど単純ではありません。
このページはコアMoodleでTeXを使用することにのみ焦点を当てています。上級ユーザに適している可能性のあるMoodleコミュニティの他のツールを含む、TeXエディタとフィルタの設定の詳細については、このページの下部にあるリンクを参照してください。
警告: このWiki環境は、特に制御シーケンスに関しては、Moodleとは異なるTeXレンダラーを使用します。このため、Moodleでどのように表示されるかを表すために画像が使用されることがあります。 YMMV。
言語の慣習
テキスト内のTeXシーケンスを識別するには、$$マーカーで囲みます。特定のコマンドまたは制御シーケンスを呼び出すには、バックスラッシュ記号\を使用します。典型的な制御シーケンスは次のようになります。
$$ x\ =\ \frac{\sqrt{144}}{2}\ \times\ (y\ +\ 12) $$
| 分数と平方根。 |
末尾の文字なしで\を使用して、方程式に追加のスペースを配置できます。
方程式は独自の行に表示されます
方程式が$$マーカーのペアで囲まれている場合、方程式はそれ自体の線の中央に表示されます。 $$は原始的なTeXマーカーです。 LaTeXでは、$$マーカーではなく、ペア\[と\]を使用して方程式を囲むことをお勧めします。これは、新しい構文が誤って入力された方程式をチェックし、垂直方向の間隔をより適切に調整するためです。 LaTeXレンダラを設定するTeXNotationフィルタがアクティブになっている場合、次の制御シーケンスで上記と同じ式が得られます。
\[ x\ =\ \frac{\sqrt{144}}{2}\ \times\ (y\ +\ 12) \]
ただし、数式の入力ミスがある場合は、ボックスで囲まれて表示され、間違いを示します。数式が新しい段落に表示される場合、数式の上の垂直方向のスペースは正しく調整されます。
$$…$$の代わりに\[…\]を使用すると、他の利点があります。たとえば、Wiris数式エディタがインストールされている場合、Attoエディタは$$で囲まれたTeX数式コードをXMLコードに変換しますが、数式が\[および\]で囲まれている場合は変換されません。
テキスト内に表示される方程式
TeX表記法フィルタをアクティブにすると、方程式が\(と\)のペアで囲まれている場合、方程式がテキスト内に表示されます。たとえば、次のようになります。
ポイント\( \left( {{x}_{0}}+\frac{1}{p\left( {{x}_{0}} \right)}\ ,\ \frac{q\left( {{x}_{0}} \right)}{p\left( {{x}_{0}} \right)} \right) \)が見つかりました...
次のように表示されます。
単一の$マークはこの目的では機能しない場合があることに注意してください。
予約文字とキーワード
キーボードのほとんどの文字と数字は、デフォルト値で使用できます。ただし、他のコンピューティング言語と同様に、プログラムが独自の目的で使用する予約文字とキーワードのセットがあります。 TeX表記法も例外ではありませんが、予約文字のセットはごくわずかです。これは予約文字の完全なリストではありませんが、これらのいくつかは次のとおりです。
@ # $ % ^ & * ( ) .
これらの文字を方程式で使用するには、\$や\%のようにそれらの前に\を配置するだけです。バックスラッシュを使用する場合は、\backslashを使用してください。ここでの唯一の例外は、&、アンパサンドのようです。
上付き文字、下付き文字、および平方根
上付き文字は、キャレット、^、記号を使用して記録されます。数学クラスの例は次のとおりです。
$$ 4^2 \ \times \ 4^3 \ = 4^5 $$
これは簡単な言い方です:
(4 x 4) x (4 x 4 x 4) = (4 x 4 x 4 x 4 x 4)
または
16 x 64 = 1024.
下付き文字も同様ですが、アンダースコア文字を使用します。
$$ 3x_2 \ \times \ 2x_3 $$
上付き文字または下付き文字が必要な場合はこれで問題ありませんが、平方根は少し異なります。これは制御シーケンスを使用します。
$$ \sqrt{64} \ = \ 8 $$
これをもう少し進めることもできますが、制御文字を追加します。次のような質問をすることができます。
$$ If \ \sqrt[n]{1024} \ = \ 4, \ what \ is \ the \ value \ of \ n? $$
これらのさまざまなコマンドを使用すると、次のような方程式を作成できます。
$$ The \sqrt{64} \ \times \ 2 \ \times \ 4^3 \ = \ 1024 $$
上付き文字、下付き文字、および平方根は、行列。
分数
ルールを覚えている限り、TeXの分数は実際には単純です。
$$ \frac{numerator}{denominator} $$ which produces
これは次のように与えることができます:
.
これは次のように入力されます。
$$ \frac{5}{10} \ is \ equal \ to \ \frac{1}{2}.$$
分数を使用すると(他のコマンドと同様に)、中括弧をネストできるため、たとえば、負の指数を分数で実装できます。ご覧のように、
$$\frac {5^{-2}}{3}$$ will produce
$$\left(\frac{3}{4}\right)^{-3}$$ will produce and
$$\frac{3}{4^{-3}}$$ will produce
$$\frac{3}{4}^{-3}$$ は を生成するため使用したくない場合があります。
行列で分数と負の指数を使用することもできます。
ブラケット
学生が数学を進めると、ブラケットと接触します。代数表記は括弧に大きく依存します。 (および)の通常のキーボード値は、次のように役立ちます。
これは次のように書かれています:
$$ d = 2 \ \times \ (4 \ - \ j) $$
通常、これらの角括弧はほとんどの数式に十分ですが、状況によってはそうではありません。このことを考慮:
は大丈夫ですが、次のようにしてみてください。
これは、次の方法で実現できます。
$$ 4x^3 \ + \ \left(x \ + \ \frac{42}{1 + x^4}\right) $$
代わりに\left(および\right)記号を使用した単純な変更。実際の括弧には名前と表示の両方があることに注意してください。ブラケットは行列。
省略記号
省略記号は単純なコードです。
次のように書かれています:
$$ x_1, \ x_2, \ \ldots, \ x_n $$
より実用的なアプリケーションは次のとおりです。
問題: "1\ldots38のすべての数字を合計します。 この問題に対するエレガントでシンプルな解決策は何ですか? この解決策を説明する代数関数を作成できますか? あなたの解答はすべての数字で機能しますか?"
解答: この問題では、偶数を使用して数学的なプロセスを示し、代数式を生成します。
| Part 1: | Part 2. | Part 3. |
|
|
代数関数は次のようになります。
ここで、t =合計、n =最後の数値です。 |
解決策は、最大数と最小数を使用して、数を加算し、次に異なる組み合わせの数を掛けて、最初と最後の数を加算して同じ結果を生成することです。
答えは数に依存する必要があります、 整数であること。したがって、このソリューションは奇数の範囲では機能せず、偶数の範囲でのみ機能します。 |
記号
これらは、MoodleのTeX表記法で利用できるすべての記号ではなく、Moodleで機能することがわかった記号だけです。
| \amalg | \cup | \oplus | \times | ||||
| \ast | \dagger | \oslash | \triangleleft | ||||
| \bigcirc | \ddagger | \otimes | \triangleright | ||||
| \bigtriangledown | \diamond | \pm | \odot | ||||
| \bigtriangleup | \div | \ominus | \wr | ||||
| \circ | \wedge | \vee | \sqcup | ||||
| \leq | \geq | \equiv | \prec | ||||
| \succ | \sim | \perp | \preceq | ||||
| \succeq | \simeq | \mid | \ll | ||||
| \gg | \asymp | \parallel | \subset | ||||
| \supset | \subseteq | \supseteq | \approx | ||||
| \neq | \ni | \notin | \in | ||||
| \vdash | \dashv | \bullet | \cdot |
矢印
| \leftarrow | \longleftarrow | \Leftarrow | \Longleftarrow | ||||
| \rightarrow | \longrightarrow | \Rightarrow | \Longrightarrow | ||||
| \uparrow | \Uparrow | \downarrow | \Downarrow | ||||
| \leftrightarrow | \longleftrightarrow | \updownarrow | \Updownarrow | ||||
| \Leftrightarrow | \Longleftrightarrow | \leftrightharpoons | \Im | ||||
| \nearrow | \nwarrow | \swarrow | \searrow |
区切り文字と数学の構成
注:ほとんどの区切り文字と構成要素は、適切に表示されるために追加のパラメーターが必要です。
| \{x | \} | \rangle | \langle | ||||
| \angle | \= | \sqrt{ab} | \sqrt[n]{ab} | ||||
| \frac{ab}{cd} | \backslash | \widehat{ab} | \$ | ||||
| \overline{ab} | \underline{ab} | \therefore | \ddots | ||||
| \% | \# | \vdots | \emptyset |
警告:LaTeXの&文字には、通常、バックスラッシュ記号\が必要です。 TeX Notation for Moodleでは、明らかにそうではありません。他のパッケージ、AsciiMathは、それを再び異なる方法で使用する可能性があるため、使用には注意してください。著作権文字はMimeTeX文字セットを使用する場合があり、TeX Notation forMoodleに不可欠なパッケージを多数提供したJohnForkoshAssociatesに著作権表示を作成するので理解できます。私は、ほぼ確実に、特定の指示が異なる通知を生成することを知らされています。:)
TeX Notation for Moodleで使用できるが、このページではレンダリングされない文字もいくつかあります。
| 大きい\left(xおよび\right)角かっこ | |
| \widetilde{ab} | |
| \textdegree or (50)^\circ |
ギリシャ文字
| \alpha | \beta | \gamma | |||
| \delta | \epsilon | \zeta | |||
| \eta | \theta | \iota | |||
| \kappa | \lambda | \mu | |||
| \xi | \pi | \rho | |||
| \sigma | \tau | \upsilon | |||
| \phi | \chi | \psi | |||
| \omega | \Omega | \Theta | |||
| \Delta | \Pi | \Phi | |||
| \Gamma | \Lambda | \Sigma | |||
| \Psi | \Xi | \Upsilon | |||
| \vartheta | \varrho | \varphi | |||
| \varsigma |
注目すべき例外
ギリシャ文字のオミクロン(伝統的に、数学者はゼロと混同される可能性があるため、オミクロンをあまり使用しません)。簡単に言えば、小文字のオミクロンは "o" であり、o と呼ばれます。ただし、\omicronはMathJaxを含む最近のTeX実装で動作する可能性があることに注意してください。
執筆時点では、これらのギリシャ語の大文字は、MoodleのTeX表記法ではレンダリングできません。
アルファ、ベータ、ゼータ、イータ、タウ、チー、ムー、イオタ、カッパ、イプシロン。
TeX methematicsは、ギリシャ語の小文字の記号はイタリック体として表示され、ギリシャ語の大文字の記号は直立した文字として表示されるという規則を採用しています。したがって、欠落しているギリシャ語の大文字は、 \mathrm{ } に相当するもので簡単に表すことができます。
ブール代数
ブール(論理)代数を表すには、さまざまな規則があります。コンピュータサイエンスと電子工学で使用される一般的な規則の詳細を以下に示します。
否定、NOT、¬、!、~、−
\lnot, !, \sim, \overline{ }
接続詞、AND、∧、
\land, \wedge, \cdot
接合不全、OR、∨、+、
\lor, \vee, +
排他的論理和、XOR⊻、⊕
\veebar, \oplus
同等性、Iff、≡、↔、⇔の場合のみ
\equiv, \leftrightarrow \iff
例:ド・モルガンの法則の2つの表現:
$$ A \cdot B = \overline{\overline{A} + \overline{B}} SS
$$ (A \land B) \equiv \lnot(\lnot{A} \lor \lnot{B}) $$
フォント
特定のフォントを使用するには、上記と同じ構文を使用してフォントにアクセスする必要があります。
数学書道フォント:
または
$$ \mathcal{ABCDEFGHIJKLMNOPQRSTUVXYZ}$$
黒板太字、Castellarタイプのフォント:
または
$$ \mathbb{ABCDEFGHIJKLMNOPQRSTUVXYZ}$$
数論でよく使われます。例えば: = 0 {0、1、2、3、...}を含む自然数のセット、 =整数のセット{-...、-3、-2、-1、0、1、2、3、...}、 =整数を含む有理数のセット、 =実数のセット。これには、自然数、有理数、および無理数が含まれます。
古英語タイプのフォントであるFraktur:
または
$$ \mathfrak{ABCDEFGHIJKLMNOPQRSTUVXYZ}$$
これは、MoodleのTex Notationでは、他の完全なTeXパッケージの場合とは異なります。
イタリックフォント:
または
$$ \mathit{ABCDEFGHIJKLMNOPQRSTUVXYZ} $$
通常の直立した非イタリックのローマンフォント:
または
$$ \mathrm{ABCDEFGHIJKLMNOPQRSTUVXYZ} $$ 太字フォント:
または
$$ \mathbf{ABCDEFGHIJKLMNOPQRSTUVXYZ} $$
ディスプレイのサイズ
デフォルトのサイズは、通常のフォントサイズより少し大きくレンダリングされます。 MoodleのTeX表記法は、"小さい" から "大きい" までの8つの異なるサイズを使用します。ただし、これらの値は異なる意味を持っているようであり、ユーザの画面解像度に依存していると思われます。サイズは4つの異なる方法で記録できます。
| \fontsize{0} to \fontsize{7} | $$\fontsize{2} x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12)$$ | |
| \fs{0} to \fs{7} | $$\fs{4} x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12)$$ | |
| \fs0 to \fs7 | $$\fs6 x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12)$$ | |
| As well, you can use \tiny \small
\normalsize \large \Large \LARGE \huge \Huge |
$$\normalsize x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12)$$ |
MoodleのTeX表記法により、\fs6、\fs7、\huge、および\Hugeを適切にレンダリングできるようになりました。
色
多くのスクリプト言語とは異なり、使用する色に名前を付けるだけで済みます。色を少し試してみる必要があるかもしれませんが、ページが明るくなります。名前を付けると、ステートメント全体がその色で表示されます。色を混在させると、最後に名前が付けられた色が優先されます。いくつかの例:
| $$ \red x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12) $$ | |
| $$ \blue x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12) $$ | |
| $$ \green x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12) $$ | |
| $$ \red x \ = \ \frac{\sqrt{144}}{2}$$ $$ \times $$
$$\green (y \ + \ 12) $$ $$ \ = $$ $$ \ \blue 6^3 $$ |
Moodle 2.2注:これはあなたにとってうまくいかないかもしれません。 tex表記法設定 "LaTeXプリアンブル"(サイト管理/プラグイン/フィルタ/ TeX表記法の下)に "\usepackage{color}" を追加してから、次の新しい構文を使用できます。$$ \color{red} x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12) $$
あなたはこれが最後のものに気付くかもしれません、それは色のために前のものよりかなり複雑です。 WindowsのTeX表記法では、多色の数式は使用できません。数式で複数の色に名前を付けると、最後に名前が付けられたものだけが使用されます。
幾何学的形状
幾何学的形状を作成するには、円を使用する方法と線を使用する方法の2つがあります。それぞれが正しくなるには少し練習が必要ですが、いくつかの単純なジオメトリを提供できます。 IllustratorやPaintShop Pro、または他の多くの描画パッケージのいずれかで形状を作成し、それらを使用してレッスンを説明する方が簡単な場合がありますが、Moodleのいくつかの簡単な図の方がうまくいく場合があります。
サークル
サークルは簡単に作成できます。
| 円は簡単に作成でき、円の大きさを決定するために必要なのは数字だけです。
サークルを作成するには、$$ \circle(150) $$を使用します。これにより、直径150ピクセルの円が作成されます。 |
円弧の作成
円弧も簡単に作成できますが、いくつかの追加パラメータが必要です。円で使用されているのと同じコード構造で基本的な形状が作成されますが、始点と終点を含めると円弧のみが作成されます。ただし、0点が真北ではなく東にあり、反時計回りに走っているところに注意してください。
| $$ \circle(120;90,180)$$ | $$ \circle(120;0,90)$$ | ||
| $$ \circle(120;180,270)$$ | $$ \circle(120;270,360)$$ |
この構造は、\circleコマンド、円の半径ではなく直径、セミコロン、円弧の境界、0、東、出発点からの度数での始点と終点の指定に分解されます。キャンバスは、円のパラメータで指定された直径のサイズであることに注意してください。
\pictureコマンド
上に示したように円と円弧を使用することは、いくらか制限があります。 \pictureコマンドを使用すると、フレームを使用して多くのレイヤーの画像を作成できます。ただし、画像の各部分は独自のスペースに配置する必要があります。このフレームを使用すると、ある程度クリエイティブになりますが、使用に関しては非常に厳格で迅速なルールがいくつかあります。
画像のすべての要素は、画像フレーム内に配置する必要があります。たとえば、円弧の一部がフレームの境界を越えた場合、予期しない結果が発生します。 (これは、次に説明する線に特に当てはまります。境界線を踏み越えた結果、深刻な問題が発生する可能性があります。)
\pictureコマンドは次のように構成されています。
\picture(100){(50,50){\circle(200)}}
\command(size of frame){(x co-ordinate, y co-ordinate){\shape to draw(size or x co-ordinate, y co-ordinate)})
注: 中括弧は、必要な開始点座標の各セットを囲むために使用されます。中括弧の各セット内では、別の括弧のセットを使用して座標の各セットを他の座標から分離し、それらの座標は適切な角かっこと円記号を使用します。開閉ブラケットを数え、位置に注意してください。
| $$ \picture(100){(50,50){\circle(200)}}&&
ピクチャーフレームは、他の方法では見ることができない要素をまとめています。 フレームサイズが100pxで、円の中心点がフレームの中点にあるため、200pxの円は押しつぶされます。サイズが正しくない場合、予期しない結果が発生します。 |
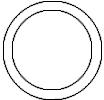
ピクチャーフレームを使用して、円を重ねることができます と線が互いに重なり合うか、交差する可能性があります。 $$ \picture(100){(50,50){\circle(99)} (50,50){\circle(80)}} $$ | ||
| 中央にドットが付いた円の画像を見たい場合があります。
中央のドットを正しく配置する必要があるかもしれませんが、 画像内の要素の順序が影響を与える可能性があります。 $$ \picture(100){(48,46){\bullet}(50,50){\circle(99)}} $$ |
上記と同じアイデアを使用して、半円を作成できます。
$$\picture(150){(50,50){\circle(100;0,180)}(100,50){\circle(100;180,360)}}$$ |
線
警告: MoodleのTeX表記法で線を引くことは問題です。詳細については、テキスト表記の使用を参照してください。線が正しく記録されていない場合、パーサーは線を正しく描画しようとしますが、正常に完了しません。これは、描画する必要のあるすべての画像が、エラーが発生するまで描画されることを意味します。エラーが変換されているときは失敗するため、後続の画像は描画されません。次の問題または次の画像に移動する前に、注意して線が機能することを確認してください。
| $$\red \picture(200){(20,0){ \line(180,0)}{(20,180){\line(180,0}$$
画像ボックスの構造は、\picture(200)が正方形の画像テンプレートを提供することです。 (20,0) は、後続の行の開始座標を提供します。この場合、開始点はx軸が20ピクセル、y軸が0ピクセルです。すべての座標の開始点である0,0は左下隅であり、時計回りに実行されます。 これを円弧と混同しないでください。 \line(180,0) は、線の長さと傾きを決定します。この場合、傾きは0で、長さは180pxです。 これらは中括弧で囲まれ、すべて \picture() 制御シーケンスが所有する1セットの中括弧内にあります。 次のコマンドセットは同じです。つまり、(20,200) は次の行の座標です。 x座標は20、つまり0点から右への距離です。 y座標は、画像の下部からの距離です。最初の線は画像フレームの下部で開始および実行されましたが、y座標は画像の下部から200ピクセルのマークで開始します。長さが180ピクセルで、yの傾きがない線。これにより、平行線のスプレッドペアが作成されます。 |
これは線の構造を説明していますが、それらをさらに活用するために通過する必要のある要素がいくつかあります。
正方形と長方形
正方形と長方形の描画は似ていますが、わずかに異なります。
四角い箱の道具があるはずですが、中に何かが入っていないと表示されません。 \lineコマンドを使用して正方形を作成する方が実際には簡単です。
| このボックスは以下を使用して構築されています。
$$ \picture(250){(10,10){\line(0,230)}(10,10){\line(230,0)}(240,10){\line(0,230)}(10,240){\line(230,0)}}$$ これは、内部に230ピクセルの正方形がある250ピクセルの正方形のボックスです。 |
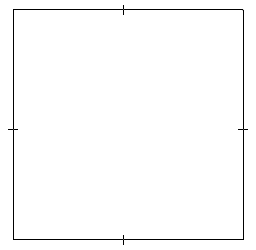
このボックスは、正方形で使用される同じ長さのインジケーターがあるという点で異なります。
$$ \picture(250){(10,10){\line(0,230)} (5,120){\line(10,0)} (10,10){\line(230,0)} (120,5){\line(0,10)} (240,10){\line(0,230)} (235,120){\line(10,0)} (10,240){\line(230,0)} (120,235){\line(0,10)}}$$ | ||
| 長方形は同じものになりますが、片側が短くなります。ポートレートキャンバスの場合、次のようになります。
$$ \picture(250){(10,10){\line(0,230)}(10,10){\line(150,0)}(160,10){\line(0,230)}(10,240){\line(150,0)}}$$ |
長方形は横向きの形状を生成することもできます。
$$ \picture(250){(10,10){\line(0,160)}(10,10){\line(230,0)}(240,10){\line(0,160)}(10,170){\line(230,0)}}$$ |
角度の制御
角度の制御は少し異なります。それらは異なる認識を含みますが、なじみのないものではありません。このことを考慮:
ある角度で線を引きたい点があります。この時点で使用される表記は、正、正または正、負または負、正または負、負にすることができます。有向数を使用して、それを数平面またはグラフのように考えてください。 0,0ポイントは中央にあり、その周りに4つの象限があり、前述の結果の1つが得られます。
| $$\picture(100){(50,50){\line(40,45)}}$$,
正のxと正のy | |
| $$\picture(100){(50,50){\line(-40,45)}}$$
負のxと正のy | |
| $$\picture(100){(50,50){\line(-40,-45)}}$$
負のxと負のy | |
| $$\picture(100){(50,50){\line(40,-45)}}$$
正のxと負のy |
基本的に、これらのポイントの要約は、挿入ポイントより上にあるものはすべてy軸上で正であり、下にあるものはすべて負であるということです。挿入ポイントの左側はすべてマイナスで、右側はすべてプラスです。
| $$\picture(100){(50,50){\line(40,45)}(50,50){\line(-40,45)}(50,50){\line(-40,-45)}(50,50){\line(40,-45)}}$$
TeXの座標アライメントプロセスは、すべてのラインの単一の開始点として1セットの座標を使用できるほど良くありません。各オブジェクトのレイヤーは、前のオブジェクトの位置によって異なるため、各オブジェクトを正確に配置する必要があります。 この座標構造は、交差する線、平行線、三角形に大きな影響を与えます。 |
交差する線
\pictureコントロールシーケンスを使用すると、交差するペアを簡単に設定できます。
| $$ \picture(200){(10,0){\line(150,150)} (0,130){\line(180,-180)}} $$
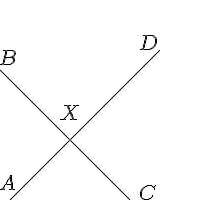
描かれた線にはラベルを付けることができます。 $$ \picture(200){(10,0){\line(150,150)}(0,130){\line(180,-180)} (0,10){A}(0,135){B}(140,0){C}(140,150){D}(62,80){X}} $$ 別の画像を作成します。 |
||
| あなたが質問したいかもしれません:
$$The \ \angle \ of \ AXB \ is \ 72\textdegree. \ What \ is \ the \ value \ of \ \angle BXD? $$ 注:右上のこの画像のラベル付けは、かなり簡単であることがわかりました。線の始点または終点で点を数ピクセルオフセットすることは、成功した戦略であることが証明されました。 Xポイントはもう少し問題があることがわかり、正しくする前にいくつかの調整を行いました。ここでの経験が役立ちます。 | ||
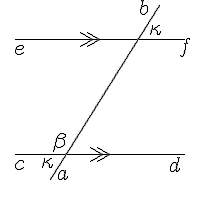
| ラベルを使用すると、描画は従来の幾何学的な描画に少し似たものになる可能性がありますが、細部には悪魔がいます。平行マーカーは適切に配置する必要があり、そこで経験が実際に出てきます。垂直または水平の線では、キーボードから直接 > または < を使用するか、またはまたはシンボル。いずれの場合も、適切に配置する必要があります。
コード: $$\picture(200){(15,45){\line(170,0)} (15,30){c}(170,28){d}(15,160){\line(170,0)}(15,145){e}(180,143){f}(50,20){\line(110,175)}(58,20){a}(140,185){b}(42,32){\kappa}(53,48){\beta} (150,165){\kappa} (90,38){\gg}(80,153){\gg} }$$ |
||
線と円弧
線と円弧を組み合わせるのは、実際には多くのレベルで深刻な課題です。たとえば、円の最初のページから円弧を取りましょう。
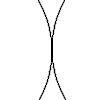
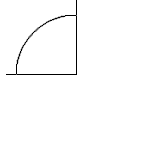
| それ自体はかなり無害ですが、要素を追加し始めると、劇的に変化します。
$$ \circle(120;90,180) $$ | |
| $$\picture(150){(75,75){\circle(120;90,180)}(75,75){\line(-70,0)}(75,75){\line(0,75)}} $$
この図面のすべての要素は同じ場所から始まります。それぞれがレイヤー化され、キャンバス上に適切に配置され、同じ座標を使用して開始すると、それらを簡単に制御できます。円弧のサイズに関係なく、交差する線はすべて円弧の中心座標を使用して描画できます。 |
三角形
すべての描画オブジェクトの中で、実際に最も困難なのは三角形です。例えば:
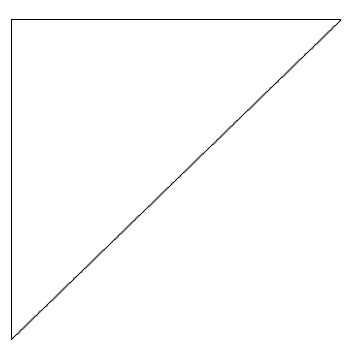
|
$$\picture(350){(10,10){\line(0,320)}(10,330){\line(330,0)}(10,10){\line(330,320)}}$$ |
これは単純な三角形であり、辺の単純なルールセットを確立することができます。垂直方向には常にx=0の座標があり、水平方向には常にa y=0の座標があります。
この場合、水平方向のx値が330、垂直方向のa y値が320の場合、斜辺の値はx=340、y=330になりますが、実際にはx=330およびa y=320になります。 線のx値とy値に開始点の座標を追加する必要はありません。 |
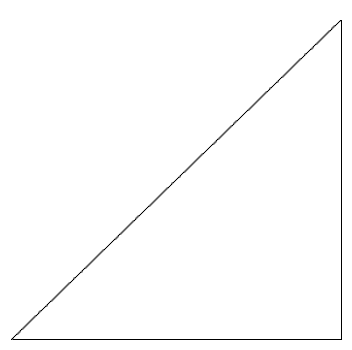
$$picture(350){(10,10){\line(330,0)}(340,10){\line(0,320)}(340,330){\line(-330,-320)}}$$ |
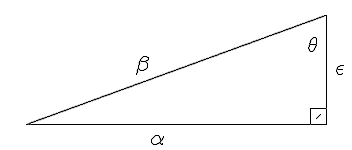
この三角形は三角法ページ用に開発されましたが、追加の表記法により、どのように使用できるかについての洞察が得られるはずです。
| これはラベル付きの画像ですが、小さな線が入った\ fboxが含まれています。少しの努力で、2本の交差する短い線に置き換えることができます。
$$\picture(350,150){(25,25){\line(300,0)}(325,25){\line(0,110)}(25,25){\line(300,110)}(309,25){\fbox{\line(5,5)}} (307,98){\theta}(135,75){\beta}(150,5){\alpha}(335,75){\epsilon}}$$ |
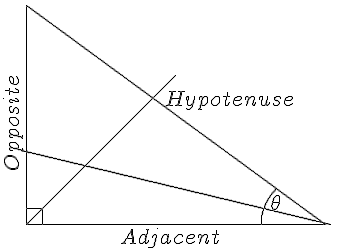
| 三角形は次のように表示されます。 | 三角形のさまざまな要素を使用して、直角三角形について知っておく必要のあることを識別します。
斜辺は常に直角の反対側です。最も長い辺は常に斜辺です。 三角形の他の要素を識別するために、記号を探します。 は反対側に名前を付けるための開始点です。 の反対側は反対側として知られています。 の横にある側は、隣接側と呼ばれます。 どちらがどちらかを判断するには、二等分する線を引きますそしてそれが交差するどんな線も反対側です。 |
| コード:
$$ \picture(350,250){(25,25){\line(300,0)}(25,25){\line(0,220)}(25,245){\line(300,-220)}(310,25){\circle(100;135,180)}(20,100){\line(310,-75)} (25,25){\fbox{\line(5,5)}}(25,25){\line(150,150)}(165,140){Hypotenuse}(120,2){Adjacent}(2,80){\rotatebox{90}{Opposite}}(270,40){\theta}}$$ | |
行列
マトリックスは、数値情報を整理するために使用できる行と列に配置された数値の長方形配列です。マトリックスを使用して、実際の状況、つまりポーリングの傾向と結果を予測できます。
マトリックス
この場合、マトリックスは、配列を作成する前に角かっこを使用して作成されます。
$$ M = \left[\begin{array}{ccc} a&b&1 \ c&d&2 \ e&f&3\end{array}\right] $$
配列の内部構造は、&、アンパサンド、および二重円記号によって生成されます。
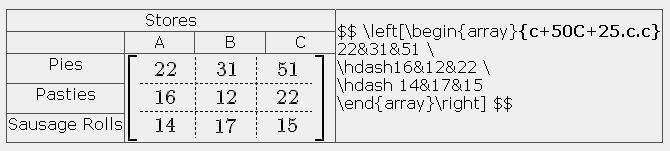
マトリックスのグリッドを作成することもできます。
ここでのコマンドシーケンスは、{c|c.c} と\hdashおよび\hlineです。パイプ、|、およびピリオドによって、垂直線の線種が決まります。
マトリックスは、サイズや色などの他のTeX表記法コマンドにも応答します。
等しい行列と等しくない行列の作成
等しい行列と等しくない行列は、同じ数の行と列を共有する、または共有しない単純な行列です。より正確には、等しい行列は同じ次数を共有し、対応する位置の各要素は等しくなります。それ以外は不等行列です。
実際には、等しい行列と等しくない行列は同様の線に沿って作成されますが、形状は異なります。
マトリックスのラベル付け
足し算と引き算の行列も似ていますが、通常、表現は大きく異なります。問題は、ラベルを配列に混在させようとするときに発生します。 TeX表記法の洗練されていないことは、ここでそれと対立します。
Moodleはテーブルを簡単に採用して機能させることができます。例えば:
パン屋のビルは、A、B、Cの3つのショップにパイ、パスティ、ソーセージロールを提供しています。 彼は、供給の見積もりにおいて、これら3つのショップの在庫レベルを決定することが期待されています。
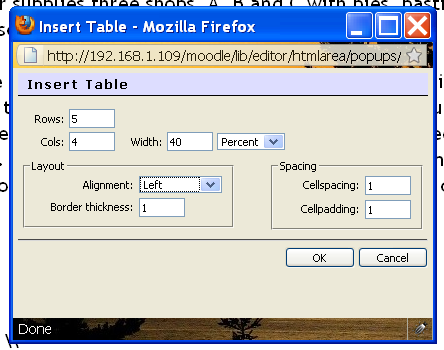
これにはMoodleフルスクリーンエディタを使用して、最終製品がどのように見えるかをよりよく理解し、利用可能な追加のツールを利用することをお勧めします。設計上の決定は、しばらくの間私たちの注意を引く必要があります。 5行4列のテーブルが必要です。最初の行はヘッダー行であるため、ラベルは中央に配置されます。次の行には4つの列が必要で、開始する空白のセルとラベルA、B、Cが必要です。次の3つの行は2つの列に分割され、最初の列とマトリックスの各行にラベル、パイ、ペースト、ソーセージロールがあります。そこにマージされた列のセットに存在します。したがって、最初にテーブルを作成します。
| テーブルの挿入-初期プロパティ | セルの結合ボタン | 高度なプロパティ |
|
|

|
| これを機能させるには、テーブルとセルの詳細プロパティ設定を調べる必要がある場合があります。 | ||
これは即時の結果です:
見栄えはあまり良くありませんが、詳細設定ボタンとプロパティボタンを使用してテーブルを微調整すると、マトリックス自体を微調整できます。
マトリックスの微調整
"c" は "column" を表すのではなく、実際には "centre" を表すことに注意してください。列は、左がl、中央がc、右がrの文字で整列されます。
各列は50ピクセルに分散しているため、50の値が配置宣言に入力されます。値の前のプラス記号は、行列全体に値を "伝播" または強制するために使用されますが、1つの列のみを分離する場合は使用されません。
行を設定することはもう少し問題があります。大文字のCは、垂直方向の配置を中心に設定します(Bはベースライン用ですが、数値がベースラインに表示されることを保証するものではなく、3番目の値は表示されません)。プラス記号とそれに続く値は、すべての行の高さを指定された数値に設定します。これでは、マトリックス全体に対して25ピクセルの値を指定しました。 4列または5列の場合、同じ高さの要件があります。
表示される順序も重要です。これらの設定の順序を変更すると、まったく機能しないか、期待どおりにレンダリングされません。何かが正しく機能しない場合は、最初に正しい順序になっていることを確認してください。
追加マトリックス
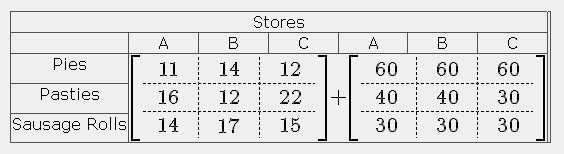
行列に対して演算を実行するための規則は、それらが等しい行列でなければならないということです。たとえば、加算行列は次のようになります。
結果は明らかです。コードは次のとおりです。
$$\left[\begin{array}{c+50C+25.c.c}
11&14&12 \ \hdash16&12&22 \ \hdash 14&17&15
\end{array}\right] + \left[\begin{array}{c+50C+25.c.c}
60&60&60 \ \hdash 40&40&30 \ \hdash 30&30&30
\end{array}\right] $$
減算行列
その構築における加算行列と同様に、減算行列は同じ等式の規則に従います。
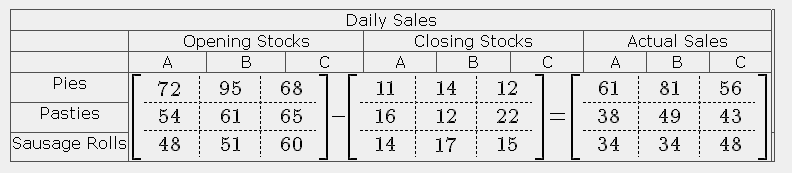
同じ重要なデータを使用して、各ショップの1日あたりの売上を計算できます。
コードは次のとおりです。
$$ \left[\begin{array}{c+50C+25.c.c}
72&95&68 \ \hdash 54&61&65 \ \hdash 48&51&60
\end{array}\right] - \left[\begin{array}{c+50C+25.c.c}
11&14&12 \ \hdash 16&12&22 \ \hdash 14&17&15
\end{array}\right] = \left[\begin{array}{c+50C+25.c.c}
61&81&56 \ \hdash 38&49&43 \ \hdash 34&34&48
\end{array}\right] $$
このコードは実際よりも複雑に見え、行とアラインメントシーケンスによって乱雑になっています。
乗算行列
加算行列または減算行列とは異なり、乗算行列は、行行列、列行列、および回答行列の3つの部分で構成されます。これは、それが異なる構築方法を持っていることを意味します。
そして、このためのコードは次のとおりです。
$$ \begin{array} 10&14&16\end{array} \
\left[\begin{array} 45 \\ 61 \\ 19 \end{array}\right]
\ = \ \begin{array} 450&854&304\end{array} $$
違いはありますが、必ずしも複雑ではありません。たとえば、次のような問題があります。
パン屋のビルは、彼の製品をカフェのオーナーであるコンに販売しています。 コンは、彼の全体的な価格が自分にとって有益であることを確認したいと考えています。 コンは彼の平均価格が十分に提供していることを確認する必要があります カフェを開いたままにしておくことができる利益。 コンは彼の計算をします 週単位で、コストと販売価格を比較します。
パイ、パスティ、ソーセージロールをこの順序で使用して、コストと販売価格の列に適用します。
このためのコードは次のとおりです。
$$\left[\begin{array} 350&310&270 \end{array}\right] \
\left[\begin{array} \$2.10&\$3.60 \ \$2.05&\$3.60 \ \$1.90&\$3.10 \end{array}
\right] \ = \ \left[\begin{array} \$735.00&\$1260.00 \ \$635.50&\$1116.00 \
\$513.00&$\837.00 \end{array}\right] $$
長いMathJax方程式をラップする方法
このドキュメントを参照してください。
追加
CommonHTML: { linebreaks: { automatic: true } },
"HTML-CSS": { linebreaks: { automatic: true } },
SVG: { linebreaks: { automatic: true } }
フィルタ設定の "filter_mathjaxloader | mathjaxconfig" に移動します。ダッシュボード > サイト管理 > プラグイン > フィルタ > MathJaxトリックを実行しているようです。
関連項目
- 数学ツールFAQ
- MathJaxフィルタ-Moodle2.7以降で利用可能
- TeX表記法フィルタ TeX表記法をオンにするには
- DragMath数式エディタ
- mhchemを使用した化学表記



![{\displaystyle If\ {\sqrt[{n}]{1024}}\ =\ 4,\ what\ is\ the\ value\ of\ n?}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/de3f744b77dec1df89882f592e0ac60db89f63ec)






































































































![{\displaystyle {\sqrt[{n}]{ab}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/bbdd8f05f4d794abf4cccf685bf65c5f5776b98b)