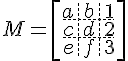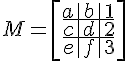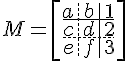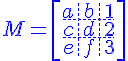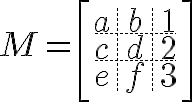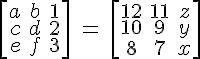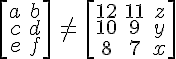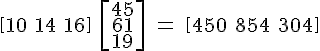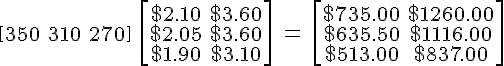Using TeX Notation
Note: This page is a work-in-progress. Feedback and suggested improvements are welcome. Please join the discussion on moodle.org or use the page comments.
TeX (/'tɛx/tekh, often pronounced TeK in English) is a very widespread and popular way of representing Mathematics notation using only characters that you can type on a keyboard (see Wikipedia). This makes it a useful format to use in Moodle, since it can be entered anywhere you can type text, from forum posts to quiz questions.
TeX expressions can be entered in multiple ways:
- typing them directly into texts.
- using the Java-based Dragmath editor in Moodle's TinyMCE editor.
- using the HTML-based equation editor in Moodle's Atto editor (since Moodle 2.7).
Afterwards, TeX expressions are rendered into Mathematics notation:
- using the TeX filter in Moodle, which uses a TeX binary installed on the server to convert expressions into .gif images (or if that is not available, it falls back to a simple built-in mimetex binary).
- using the MathJax_filter which identifies TeX expressions and uses the Mathjax JS library to render them in browsers at display time (since Moodle 2.7).
- using other third-party solutions.
As you can imagine, the whole field is not as simple as we would like, especially because there are many flavours of TeX and slight variations between tools.
This page focusses only on using TeX in core Moodle. See the links at the bottom of this page for more information on setting up TeX editors and filters, including other tools from the Moodle community that may be suitable for advanced users.
WARNING: This Wiki environment uses a DIFFERENT TeX renderer to Moodle, especially when it comes to control sequences. For this reason images are sometimes used to represent what it should look like in Moodle. YMMV.
Language Conventions
To identify a TeX sequence in your text, surround it with $$ markers. To invoke a particular command or control sequence, use the backslash, \. A typical control sequence looks like:
$$ x\ =\ \frac{\sqrt{144}}{2}\ \times\ (y\ +\ 12) $$
| Fraction and square root. |
Additional spaces can be placed into the equation using the \ without a trailing character.
Equation displayed on its own line
When an equation is surrounded by a pair of $$ markers, it is displayed centered on its own line. The $$’s are primitive TeX markers. With LaTeX, it is often recommended to use the pair \[ and \] to enclose equations, rather than the $$ markers, because the newer syntax checks for mistyped equations and better adjusts vertical spacing. If the TeX Notation filter is activated, which set a LaTeX renderer, the same equation as above is obtained with the following control sequence:
\[ x\ =\ \frac{\sqrt{144}}{2}\ \times\ (y\ +\ 12) \]
However, if the equation is mistyped, it will be displayed enclosed in a box to signal the mistake and if the equation appears in a new paragraph, the vertical space above the equation will adjust correctly.
Using \[ … \] instead of $$ … $$ may have other advantages. For example, with the Wiris equation editor installed, the Atto editor undesirably transforms the TeX code of equations enclosed with $$ into XML code, whereas it does not do so when the equations are enclosed with \[ and \].
Equation displayed within text
With the TeX notation filter activated, an equation is displayed within the text when it is surrounded by the pair \( and \). For example, the following:
The point \( \left( {{x}_{0}}+\frac{1}{p\left( {{x}_{0}} \right)}\ ,\ \frac{q\left( {{x}_{0}} \right)}{p\left( {{x}_{0}} \right)} \right) \) is located...
will display as follows:
Note that the single $ marks may not work for this purpose.
Reserved Characters and Keywords
Most characters and numbers on the keyboard can be used at their default value. As with any computing language, though, there are a set of reserved characters and keywords that are used by the program for its own purposes. TeX Notation is no different, but it does have a very small set of Reserved Characters. This will not be a complete list of reserved characters, but some of these are:
@ # $ % ^ & * ( ) .
To use these characters in an equation just place the \ in front of them like \$ or \%. If you want to use the backslash, just use \backslash. The only exception here seems to be the &, ampersand.
Superscripts, Subscripts and Roots
Superscripts are recorded using the caret, ^, symbol. An example for a Maths class might be:
$$ 4^2 \ \times \ 4^3 \ = 4^5 $$
This is a shorthand way of saying:
(4 x 4) x (4 x 4 x 4) = (4 x 4 x 4 x 4 x 4)
or
16 x 64 = 1024.
Subscripts are similar, but use the underscore character.
$$ 3x_2 \ \times \ 2x_3 $$
This is OK if you want superscripts or subscripts, but square roots are a little different. This uses a control sequence.
$$ \sqrt{64} \ = \ 8 $$
You can also take this a little further, but adding in a control character. You may ask a question like:
$$ If \ \sqrt[n]{1024} \ = \ 4, \ what \ is \ the \ value \ of \ n? $$
Using these different commands allows you to develop equations like:
$$ The \sqrt{64} \ \times \ 2 \ \times \ 4^3 \ = \ 1024 $$
Superscripts, Subscripts and roots can also be noted in Matrices.
Fractions
Fractions in TeX are actually simple, as long as you remember the rules.
$$ \frac{numerator}{denominator} $$ which produces .
This can be given as:
.
This is entered as:
$$ \frac{5}{10} \ is \ equal \ to \ \frac{1}{2}.$$
With fractions (as with other commands) the curly brackets can be nested so that for example you can implement negative exponents in fractions. As you can see,
$$\frac {5^{-2}}{3}$$ will produce
$$\left(\frac{3}{4}\right)^{-3}$$ will produce and
$$\frac{3}{4^{-3}}$$ will produce
You likely do not want to use $$\frac{3}{4}^{-3}$$ as it produces
You can also use fractions and negative exponents in Matrices.
Brackets
As students advance through Maths, they come into contact with brackets. Algebraic notation depends heavily on brackets. The usual keyboard values of ( and ) are useful, for example:
This is written as:
$$ d = 2 \ \times \ (4 \ - \ j) $$
Usually, these brackets are enough for most formulae but they will not be in some circumstances. Consider this:
Is OK, but try it this way:
This can be achieved by:
$$ 4x^3 \ + \ \left(x \ + \ \frac{42}{1 + x^4}\right) $$
A simple change using the \left( and \right) symbols instead. Note the actual bracket is both named and presented. Brackets are almost essential in Matrices.
Ellipsis
The Ellipsis is a simple code:
Written like:
$$ x_1, \ x_2, \ \ldots, \ x_n $$
A more practical application could be:
Question:
"Add together all the numbers from 1 38.
What is an elegant and simple solution to this problem?
Can you create an algebraic function to explain this solution?
Will your solution work for all numbers?"
Answer: The question uses an even number to demonstrate a mathematical process and generate an algebraic formula.
| Part 1: | Part 2. | Part 3. |
|
|
An algebraic function might read something like:
Where t = total and n = the last number. |
The solution is that, using the largest and the smallest numbers, the numbers are added and then multiplied by the number of different combinations to produce the same result adding the first and last numbers.
The answer must depend on the number, being a whole number. Therefore, the solution will not work for an odd range of numbers, only an even range. |
Symbols
These are not all the symbols that may be available in TeX Notation for Moodle, just the ones that I have found to work in Moodle.
| \amalg | \cup | \oplus | \times | ||||
| \ast | \dagger | \oslash | \triangleleft | ||||
| \bigcirc | \ddagger | \otimes | \triangleright | ||||
| \bigtriangledown | \diamond | \pm | \odot | ||||
| \bigtriangleup | \div | \ominus | \wr | ||||
| \circ | \wedge | \vee | \sqcup | ||||
| \leq | \geq | \equiv | \prec | ||||
| \succ | \sim | \perp | \preceq | ||||
| \succeq | \simeq | \mid | \ll | ||||
| \gg | \asymp | \parallel | \subset | ||||
| \supset | \subseteq | \supseteq | \approx | ||||
| \neq | \ni | \notin | \in | ||||
| \vdash | \dashv | \bullet | \cdot |
Arrows
| \leftarrow | \longleftarrow | \Leftarrow | \Longleftarrow | ||||
| \rightarrow | \longrightarrow | \Rightarrow | \Longrightarrow | ||||
| \uparrow | \Uparrow | \downarrow | \Downarrow | ||||
| \leftrightarrow | \longleftrightarrow | \updownarrow | \Updownarrow | ||||
| \Leftrightarrow | \Longleftrightarrow | \leftrightharpoons | \Im | ||||
| \nearrow | \nwarrow | \swarrow | \searrow |
Delimiters and Maths Constructs
NOTE: Most delimiters and constructs need additional parameters for them to appear appropriately.
| \{x | \} | \rangle | \langle | ||||
| \angle | \= | \sqrt{ab} | \sqrt[n]{ab} | ||||
| \frac{ab}{cd} | \backslash | \widehat{ab} | \$ | ||||
| \overline{ab} | \underline{ab} | \therefore | \ddots | ||||
| \% | \# | \vdots | \emptyset |
WARNINGS: The & character in LaTeX usually requires a backslash, \. In TeX Notation for Moodle, apparently, it does not. Other packages, AsciiMath, may use it differently again so be careful using it. The copyright character may use the MimeTeX charset, and produces a copyright notice for John Forkosh Associates who provided a lot of the essential packages for the TeX Notation for Moodle, so I understand. I have been, almost reliably, informed that a particular instruction will produce a different notice though .:)
There are also a number of characters that can be used in TeX Notation for Moodle but do not render in this page:
| Larger \left(x and \right) brackets | |
| \widetilde{ab} | |
| \textdegree or (50)^\circ |
Greek Letters
| \alpha | \beta | \gamma | |||
| \delta | \epsilon | \zeta | |||
| \eta | \theta | \iota | |||
| \kappa | \lambda | \mu | |||
| \xi | \pi | \rho | |||
| \sigma | \tau | \upsilon | |||
| \phi | \chi | \psi | |||
| \omega | \Omega | \Theta | |||
| \Delta | \Pi | \Phi | |||
| \Gamma | \Lambda | \Sigma | |||
| \Psi | \Xi | \Upsilon | |||
| \vartheta | \varrho | \varphi | |||
| \varsigma |
Notable Exceptions
Greek letter omicron (traditionally, mathemeticians don't make much use of omicron due to possible confusion with zero). Simply put, lowercase omicron is an "o" redered as o. But note \omicron may now work with recent TeX implementations including MathJax.
At the time of writing, these Greek capital letters cannot be rendered by TeX Notation in Moodle:
Alpha, Beta, Zeta, Eta, Tau, Chi, Mu, Iota, Kappa and Epsilon.
TeX methematics adopts the convention that lowercase Greek symbols are displayed as italics whereas uppercase Greek symbols are displayed as upright characters. Therefore, the missing Greek capital letters can simply be represented by the \mathrm{ } equivalent
Boolean algebra
There are a number of different conventions for representing Boolean (logic) algebra. Common conventions used in computer science and electronics are detailed below:
Negation, NOT, ¬, !, ~, −
\lnot, !, \sim, \overline{ }
Conjunction, AND, ∧,
\land, \wedge, \cdot
Dysjunction, OR, ∨, +,
\lor, \vee, +
Exclusive dysjunction, XOR ⊻, ⊕
\veebar, \oplus
Equivalence, If and only if, Iff, ≡, ↔, ⇔
\equiv, \leftrightarrow \iff
Example: two representations of De Morgan's laws:
$$ A \cdot B = \overline{\overline{A} + \overline{B}} SS
$$ (A \land B) \equiv \lnot(\lnot{A} \lor \lnot{B}) $$
Fonts
To use a particular font you need to access the font using the same syntax as demonstrated above.
A math calligraphic font:
or
$$ \mathcal{ABCDEFGHIJKLMNOPQRSTUVXYZ}$$
Blackboard bold, a Castellar type font:
or
$$ \mathbb{ABCDEFGHIJKLMNOPQRSTUVXYZ}$$
Often used in number theory. For example: = set of natural numbers including 0 {0, 1, 2, 3, ...}, = set of integers {-..., -3, -2, -1, 0, 1, 2, 3, ... }, = set of rational numbers, including integers, = set of real numbers, which includes the natural numbers, rational numbers and irrational numbers.
Fraktur, an Old English type font:
or
$$ \mathfrak{ABCDEFGHIJKLMNOPQRSTUVXYZ}$$
This is different in Tex Notation in Moodle than it is for other, full, TeX packages.
An italic font:
or
$$ \mathit{ABCDEFGHIJKLMNOPQRSTUVXYZ} $$
A normal, upright non-italic, Roman font:
or
$$ \mathrm{ABCDEFGHIJKLMNOPQRSTUVXYZ} $$ A bold-face font:
or
$$ \mathbf{ABCDEFGHIJKLMNOPQRSTUVXYZ} $$
Size of displays
The default size is rendered slightly larger than normal font size. TeX Notation in Moodle uses eight different sizes ranging from "tiny" to "huge". However,these values seem to mean different things and are, I suspect, dependent upon the User's screen resolution. The sizes can be noted in four different ways:
| \fontsize{0} to \fontsize{7} | $$\fontsize{2} x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12)$$ | |
| \fs{0} to \fs{7} | $$\fs{4} x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12)$$ | |
| \fs0 to \fs7 | $$\fs6 x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12)$$ | |
| As well, you can use \tiny \small
\normalsize \large \Large \LARGE \huge \Huge |
$$\normalsize x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12)$$ |
It appears that TeX Notation in Moodle now allows \fs6, \fs7, \huge and \Huge to be properly rendered.
Colour
Unlike many scripting languages, we only need to name the colour we want to use. You may have to experiment a little with colours, but it will make for a brighter page. Once named, the entire statement will appear in the colour, and if you mix colours, the last named colour will dominate. Some examples:
| $$ \red x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12) $$ | |
| $$ \blue x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12) $$ | |
| $$ \green x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12) $$ | |
| $$ \red x \ = \ \frac{\sqrt{144}}{2}$$ $$ \times $$
$$\green (y \ + \ 12) $$ $$ \ = $$ $$ \ \blue 6^3 $$ |
Moodle 2.2 note: You may find this doesn't work for you. You can try to add "\usepackage{color}" to your tex notation setting "LaTeX preamble" (under Site adminstration/Plugins/Filters/TeX notation)and then use this new syntax: $$ \color{red} x \ = \ \frac{\sqrt{144}}{2} \ \times \ (y \ + \ 12) $$
You may note this last one, it is considerably more complex than the previous for colours. TeX Notation in Windows does not allow multicoloured equations, if you name a number of colours in the equation, only the last named will be used.
Geometric Shapes
There are two ways to produce geometric shapes, one is with circles and the other is with lines. Each take a bit of practice to get right, but they can provide some simple geometry. It may be easier to produce the shapes in Illustrator or Paint Shop Pro or any one of a number of other drawing packages and use them to illustrate your lessons, but sometimes, some simple diagrams in Moodle will do a better job.
Circles
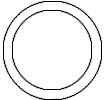
Circles are easy to make.
| Circles are easily created, and only needs a number to determine how large the circle is.
To create the circle use $$ \circle(150) $$. This makes a circle of 150 pixels in diameter. |
Creating Arcs
Arcs are also easy to produce, but require some additional parameters. The same code structure used in circles create the basic shape, but the inclusion of a start and end point creates only the arc. However, notice where the 0 point is, not at the true North, but rather the East and run in an anti-clockwise direction.
| $$ \circle(120;90,180)$$ | $$ \circle(120;0,90)$$ | ||
| $$ \circle(120;180,270)$$ | $$ \circle(120;270,360)$$ |
This structure breaks down into the \circle command followed by the diameter, not the radius, of the circle, followed by a semi-colon, then the demarcation of the arc, the nomination of the start and end points in degrees from the 0, East, start point. Note that the canvas is the size of the diameter nominated by the circle's parameters.
The \picture Command
Using circles and arcs as shown above is somewhat limiting. The \picture command allows you to use a frame in which to build a picture of many layers. Each part of the picture though needs to be in its own space, and while this frame allows you to be creative, to a degree, there are some very hard and fast rules about using it.
All elements of a picture need to be located within the picture frame. Unexpected results occur when parts of an arc, for example, runs over the border of the frame. (This is particularly true of lines, which we will get to next, and the consequences of that overstepping of the border can cause serious problems.)
The \picture command is structured like:
\picture(100){(50,50){\circle(200)}}
\command(size of frame){(x co-ordinate, y co-ordinate){\shape to draw(size or x co-ordinate, y co-ordinate)})
NOTE: The brace is used to enclose each set of required starting point coordinates. Inside each set of braces, another set of braces is used to isolate each set of coordinates from the other, and those coordinates use their proper brackets and backslash. Count the opening and closing brackets, be careful of the position,
| $$ \picture(100){(50,50){\circle(200)}}&&
The picture frame brings elements together that you may not otherwise see. Because of the frame size of 100px and the centre point of the circle in the mid-point of the frame, the 200px circle will be squashed. Unexpected results occur when sizes are not correct. |
Using the picture frame, you can layer circles and lines over each other, or they can intersect. $$ \picture(100){(50,50){\circle(99)} (50,50){\circle(80)}} $$ | ||
| You may want to see an image of a circle with a dot in the middle.
You may have to try to place the centre dot correctly , but the ordering of the elements in the image may have an impact. $$ \picture(100){(48,46){\bullet}(50,50){\circle(99)}} $$ |
Using the same ideas as above, you can make semi-circles.
$$\picture(150){(50,50){\circle(100;0,180)}(100,50){\circle(100;180,360)}}$$ |
Lines
Warning: Drawing lines in TeX Notation in Moodle is an issue, go to the Using Text Notation for more information. If the line is not noted properly then the parser will try to correctly draw the line but will not successfully complete it. This means that every image that needs be drawn will be drawn until it hits the error. When the error is being converted, it fails, so no subsequent image is drawn. Be careful and make sure your line works BEFORE you move to the next problem or next image.
| $$\red \picture(200){(20,0){ \line(180,0)}{(20,180){\line(180,0}$$
The structure of the picture box is that the \picture(200) provides a square image template. The (20,0) provides the starting coordinates for any line that comes after. In this case the start point is at 20pixels in the x axis and 0 pixels in the y axis. The starting point for all coordinates, 0,0, is the bottom left corner and they run in a clockwise manner. Do not confuse this with arcs. The \line(180,0) determines the length and inclination of the line. In this case, the inclination is 0 and the length is 180px. These are enclosed in braces, all inside one set of braces owned by the \picture() control sequence. The next set of commands are the same, that is, the (20,200) are the coordinates of the next line. The x co-ordinate is the 20, that is the distance to the right from the 0 point. The y co-ordinates is the distance from the bottom of the image. Whereas the first line started and ran on the bottom of the picture frame, the y co-ordinate starts at the 200 pixel mark from the bottom of the image. The line, at 180 pixels long and has no y slope. This creates a spread pair of parallel lines. |
While this explains the structure of a line, there is a couple of elements that you need to go through to do more with them.
Squares and Rectangles
Drawing squares and rectangles is similar, but only slightly different.
There should be a square box tool, and there is, but unless it has something inside it, it does not display. It is actually easier to make a square using the \line command.
| This box is constructed using:
$$ \picture(250){(10,10){\line(0,230)}(10,10){\line(230,0)}(240,10){\line(0,230)}(10,240){\line(230,0)}}$$ It is a 250 pixel square box with a 230 pixel square inside it. |
This box is different in that is has the equal length indicators that are used in a square.
$$ \picture(250){(10,10){\line(0,230)} (5,120){\line(10,0)} (10,10){\line(230,0)} (120,5){\line(0,10)} (240,10){\line(0,230)} (235,120){\line(10,0)} (10,240){\line(230,0)} (120,235){\line(0,10)}}$$ | ||
| The rectangle then becomes the same thing, but with one side shorter. For a portrait canvas it would be:
$$ \picture(250){(10,10){\line(0,230)}(10,10){\line(150,0)}(160,10){\line(0,230)}(10,240){\line(150,0)}}$$ |
The rectangle can also produce a landscape shape:
$$ \picture(250){(10,10){\line(0,160)}(10,10){\line(230,0)}(240,10){\line(0,160)}(10,170){\line(230,0)}}$$ |
Controlling Angles
Controlling angles is a little different. They involve a different perception, but not one that is unfamiliar. Consider this:
We have a point from which we want to draw a line that is on an angle. The notation used at this point can be positive, positive or positive, negative or negative, positive or negative, negative. Think of it like a number plane or a graph, using directed numbers. The 0,0 point is in the centre, and we have four quadrants around it that give us one of the previously mentioned results.
| $$\picture(100){(50,50){\line(40,45)}}$$,
a positive x and positive y | |
| $$\picture(100){(50,50){\line(-40,45)}}$$
a negative x and positive y | |
| $$\picture(100){(50,50){\line(-40,-45)}}$$
a negative x and negative y | |
| $$\picture(100){(50,50){\line(40,-45)}}$$
a positive x and a negative y |
Essentially, what these points boil down to is that anything above the insertion point is a positive on the y axis, anything below is a negative. Anything to the left of the insertion point is a negative while everything to the right is a positive.
| $$\picture(100){(50,50){\line(40,45)}(50,50){\line(-40,45)}(50,50){\line(-40,-45)}(50,50){\line(40,-45)}}$$
The co-ordinate alignment process in TeX is not that good that you can use one set of co-ords as a single starting point for all lines. The layering of each object varies because of the position of the previous object, so each object needs to be exactly placed. This co-ord structure has a great deal of impact on intersecting lines, parallel lines and triangles. |
Intersecting Lines
You can set up an intersecting pair easily enough, using the \picture control sequence.
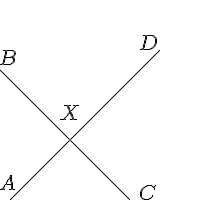
| $$ \picture(200){(10,0){\line(150,150)} (0,130){\line(180,-180)}} $$
The lines that are drawn can be labeled. $$ \picture(200){(10,0){\line(150,150)}(0,130){\line(180,-180)} (0,10){A}(0,135){B}(140,0){C}(140,150){D}(62,80){X}} $$ To produce another image. |
||
| To which you may want to ask the question:
$$The \ \angle \ of \ AXB \ is \ 72\textdegree. \ What \ is \ the \ value \ of \ \angle BXD? $$ NOTE: Labeling this image, above-right, turned out to be fairly simple. Offsetting points by a few pixels at the start or end points of the lines proved a successful strategy. The X point proved a little more problematic, and took a number of adjustments before getting it right. Experience here will help. | ||
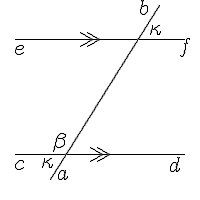
| With labels the drawing can become a little more like your traditional geometric drawing, but the devil is in the details. The parallel markers need to be placed properly, and that is where experience really comes into it. On lines that are vertical or horizontal, you can get away with using the > or < directly from the keyboard, or the or symbols. In either case, you need to position them properly.
The code: $$\picture(200){(15,45){\line(170,0)} (15,30){c}(170,28){d}(15,160){\line(170,0)}(15,145){e}(180,143){f}(50,20){\line(110,175)}(58,20){a}(140,185){b}(42,32){\kappa}(53,48){\beta} (150,165){\kappa} (90,38){\gg}(80,153){\gg} }$$ |
||
Lines and Arcs
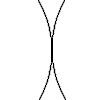
Combining lines and arcs is a serious challenge actually, on a number of levels. For example lets take an arc from the first page on circles.
| Fairly innocuous of itself, but when we start to add in elements, it changes dramatically.
$$ \circle(120;90,180) $$ | |
| $$\picture(150){(75,75){\circle(120;90,180)}(75,75){\line(-70,0)}(75,75){\line(0,75)}} $$
All elements in this drawing start in the same place. Each is layered, and properly placed on the canvas, and using the same co-ord to start makes it easy to control them. No matter the size of the arc, intersecting lines can all be drawn using the centre co-ords of the arc. |
Triangles
Of all the drawing objects, it is actually triangles that present the most challenge. For example:
|
$$\picture(350){(10,10){\line(0,320)}(10,330){\line(330,0)}(10,10){\line(330,320)}}$$ |
This is a simple triangle, one that allows us to establish a simple set of rules for the sides. The vertical always has an x=0 co-ord and the horizontal always has a y=0 co-ord.
In this case with an x value of 330 on the horizontal, and a y value of 320 on the vertical, the hypotenuse should then have a value of x=340, and the y=330, but not so, they actually have an x=330 and a y=320. There is no need to add the starting point co-ords to the x and y values of the line. |
$$picture(350){(10,10){\line(330,0)}(340,10){\line(0,320)}(340,330){\line(-330,-320)}}$$ |
This triangle has been developed for a Trigonometry page - but the additional notation should provide insight into how you can use it.
| This is a labeled image, but it has an \fbox in it with its little line. With some effort, it could be replaced with two intersecting short lines.
$$\picture(350,150){(25,25){\line(300,0)}(325,25){\line(0,110)}(25,25){\line(300,110)}(309,25){\fbox{\line(5,5)}} (307,98){\theta}(135,75){\beta}(150,5){\alpha}(335,75){\epsilon}}$$ |
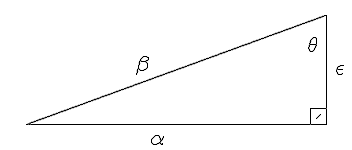
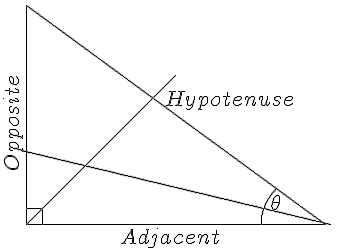
| The triangle shows like: | We use the different elements of the triangle to identify those things we need to know about a right-angled triangle.
The hypotenuse is always the side that is opposite the right angle. The longest side is always the Hypotenuse. To identify the other elements of the triangle we look for the sign . is the starting point for naming the other sides. The side that is opposite is known as the Opposite. The side that lies alongside is known as the Adjacent side. To determine which is which, draw a line that bisects and whatever line it crosses is the Opposite side. |
| The code:
$$ \picture(350,250){(25,25){\line(300,0)}(25,25){\line(0,220)}(25,245){\line(300,-220)}(310,25){\circle(100;135,180)}(20,100){\line(310,-75)} (25,25){\fbox{\line(5,5)}}(25,25){\line(150,150)}(165,140){Hypotenuse}(120,2){Adjacent}(2,80){\rotatebox{90}{Opposite}}(270,40){\theta}}$$ | |
Matrices
A Matrix is a rectangular array of numbers arranged in rows and columns which can be used to organize numeric information. Matrices can be used to predict trends and outcomes in real situations - i.e. polling.
A Matrix
A matrix can be written and displayed like 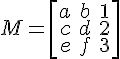
In this case the matrix is constructed using the brackets before creating the array:
$$ M = \left[\begin{array}{ccc} a&b&1 \ c&d&2 \ e&f&3\end{array}\right] $$
The internal structure of the array is generated by the &, ampersand, and the double backslash.
You can also create a grid for the matrix.
The command sequences here are the {c|c.c} and \hdash and \hline. The pipe, |, and the full stop determine the line type for the vertical line.
Matrices also respond to other TeX Notation commands such as size and colour.
Creating equal and unequal matrices
Equal and unequal matrices are simply matrices that either share or not share the same number of rows and columns. To be more precise, equal matrices share the same order and each element in the corresponding positions are equal. Anything else is unequal matrices.
Actually equal and unequal matrices are constructed along similar lines, but have different shapes:
Labeling a Matrix
Addition and subtraction matrices are similar again, but the presentation is usually very different. The problem comes when trying to mix labels into arrays. The lack of sophistication in the TeX Notation plays against it here.
Moodle allows an easy adoption of tables to make it work though. For example:
Bill the baker supplies three shops, A, B and C with pies, pasties and sausage rolls. He is expected to determine the stock levels of those three shops in his estimation of supplies.
It is better to use the Moodle Fullscreen editor for this, to have a better idea of how the end product will look and to take advantage of the additional tools available. Design decisions need occupy our attention for a while. We need a table of five rows and four columns. The first row is a header row, so the label is centred. The next row needs four columns, a blank cell to start and labels A, B and C. The next three rows are divided into two columns, with the labels, pies, pasties and sausage rolls in each row of the first column and the matrix resides in a merged set of columns there. So first the table:
| Insert Table - initial properties | Merge Cells Button | Advanced Properties |
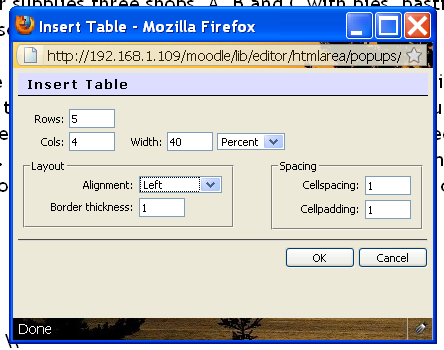
|
|

|
| You may need to look into the Advanced properties setting of the tables and cells to make this work. | ||
This is the immediate result:
While not a very good look, it can be made better by tweaking the table using the advanced settings and properties buttons and then you can tweak the matrix itself.
Tweaking the Matrix
Things are not always as they seem, be aware, the "c" does not stand for "column", it actually stands for "centre". The columns are aligned by the letters l, for left, c for centre and r for right.
Each column is spread across 50 pixels, so the value of 50 is entered into the alignment declaration. The plus sign before the value is used to "propogate" or to force the value across the whole matrix, but is not used when wanting to separate only one column.
To set the rows is a little more problematic. The capital letter C sets the vertical alignment to the centre, (B is for baseline, but that does not guarantee that the numbers will appear on the base line, and there does not appear to be any third value). The plus sign and following value sets the height of all rows to the number given. In this I have given it a value of 25 pixels for the entire matrix. If there were four or five rows, the same height requirement is made.
The order things appear is also important. If you change the order of these settings, they will either not work at all, or will not render as you expect them to. If something does not work properly, then check to make sure you have the right order first.
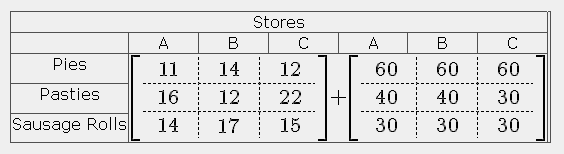
An Addition Matrix
The rule for performing operations on matrices is that they must be equal matrices. For example, addition matrices look like:
with the results obvious. The code is:
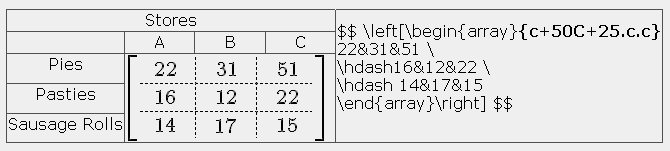
$$\left[\begin{array}{c+50C+25.c.c}
11&14&12 \ \hdash16&12&22 \ \hdash 14&17&15
\end{array}\right] + \left[\begin{array}{c+50C+25.c.c}
60&60&60 \ \hdash 40&40&30 \ \hdash 30&30&30
\end{array}\right] $$
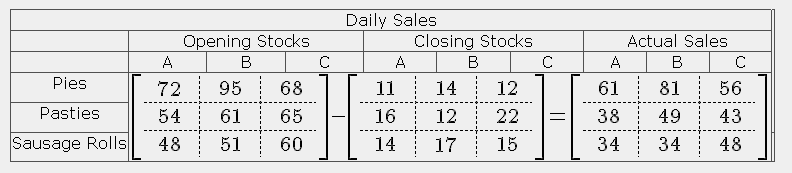
A Subtraction Matrix
Similar to an addition matrix in its construction, the subtraction matrix is subject to the same rules of equality.
Using the same essential data, we can calculate the daily sales of each of the shops.
The code is:
$$ \left[\begin{array}{c+50C+25.c.c}
72&95&68 \ \hdash 54&61&65 \ \hdash 48&51&60
\end{array}\right] - \left[\begin{array}{c+50C+25.c.c}
11&14&12 \ \hdash 16&12&22 \ \hdash 14&17&15
\end{array}\right] = \left[\begin{array}{c+50C+25.c.c}
61&81&56 \ \hdash 38&49&43 \ \hdash 34&34&48
\end{array}\right] $$
This code looks more complex than it really is, it is cluttered by the lines and alignment sequences.
Multiplication Matrices
Different than the addition or subtraction matrices, the multiplication matrix comes in three parts, the row matrix, the column matrix and the answer matrix. This implies it has a different construction methodology.
And the code for this is:
$$ \begin{array} 10&14&16\end{array} \
\left[\begin{array} 45 \\ 61 \\ 19 \end{array}\right]
\ = \ \begin{array} 450&854&304\end{array} $$
While different, it is not necessarily more complex. For example a problem like:
Bill the baker is selling his product to Con the cafe owner, who wants to make sure his overall prices are profitable for himself. Con needs to make sure that his average price is providing sufficient profit to be able to keep the cafes open. Con makes his calculations on a weekly basis, comparing cost to sale prices.
With the pies, pasties and sausage rolls in that order he applies them to the cost and sale price columns :
The code for this is:
$$\left[\begin{array} 350&310&270 \end{array}\right] \
\left[\begin{array} \$2.10&\$3.60 \ \$2.05&\$3.60 \ \$1.90&\$3.10 \end{array}
\right] \ = \ \left[\begin{array} \$735.00&\$1260.00 \ \$635.50&\$1116.00 \
\$513.00&$\837.00 \end{array}\right] $$
See Also
- Mathematics_tools_FAQ
- MathJax_filter - available in Moodle 2.7 and later
- TeX notation filter To turn on the TeX Notation
- DragMath equation editor
- Chemistry notation using mhchem



![If \ \sqrt[n]{1024} \ = \ 4, \ what \ is \ the \ value \ of \ n?](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/de3f744b77dec1df89882f592e0ac60db89f63ec)






































































































![\sqrt[n]{ab}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/bbdd8f05f4d794abf4cccf685bf65c5f5776b98b)